算法1 - 计算机科学 | Mi Manchi = yuan = Whatever is worth doing at all is worth doing well

# 差分序列

# 前言

差分序列常用于维护需要进行区间加操作的序列，但是无法做到区间查询。

# 原理

已知一组序列，用数组 a 保存。 $a_i$ 表示序列第 $i$ 个元素。建立一个数组 b，其元素取值如下：
$b_i = a_i - a_{i-1}~$

因此有 $a_1 = b_1， a_i = b_i + a_{i-1}$ ，此处在用数组的时候， $a_0 = 0$ ，下标从 1 开始存储数据

由于差分序列的性质，当我们对 $[l, r]$ 这个区间统一进行加 $d$ 操作时，只需要对

$b_l~ += d， b_{r+1} -= d$

# 代码示例

	#include <stdio.h>
	int a[5000004];
	int d[5000004];

	void add(int x, int y, int z)
	{
	d[x] += z;
	d[y + 1] -= z;
	}

	int main(void)
	{
	int n, p;//n 个数组，进行 p 次区间加操作
	scanf("%d %d", &n, &p);
	for (int i = 1; i <= n; i++)
	{
	scanf("%d", &a[i]);
	}

	// 求出初始 d 数组的值
	for (int i = 1; i <= n; i++)
	d[i] = a[i] - a[i - 1];

	// 进行 p 次区间加操作
	int x, y, z;
	for (int i = 1; i <= p; i++)
	{
	scanf("%d %d %d", &x, &y, &z);
	add(x, y, z);
	}

	// 计算最小值
	a[1] = d[1] + a[0];
	int min = a[1];
	for (int i = 2; i <= n; i++)
	{
	a[i] = d[i] + a[i - 1];
	if (min > a[i])
	min = a[i];
	}

	printf("%d", min);
	return 0;

	}

# RMQ

# 问题描述

给你一个数组，其中有 N 个数字，现在给你一次询问，给你区间 $[l ，r]$ ，问你在这个区间内的最大值为多少？

# 算法描述

# 初始化

RMQ（Range Minimum/Maximum Query），即区间最值查询。RMQ 算法一般用较长时间做预处理，时间复杂度为 O (nlogn)，然后可以在 O（1）的时间内处理每次查询。

下面我们从一个实际问题来解释 RMQ

我们假设数组 arr 为：1，2，6，8，4，3，7

我们设二维数组 dp [i][j] 表示从第 i 位开始连续个数中的最小值。例如 dp [2][1] 就表示从第二位数开始连续两个数的最小值（也就是从第二位数到第三位数的最小值），即 2，6 中的最小值，所以 dp [2][1] = 2;

其实我们求 dp [i][j] 的时候可以把它分成两部分，第一部分是从到，第二部分从到，为什么可以这么分呢？其实我们都知道二进制数前一个数是后一个的两倍，那么可以把到这个区间通过分成相等的两部分，那么转移方程很容易就写出来了。（dp [i] [0] 就表示第 i 个数字本身）

$dp[i] [j] = min(dp [i] [j - 1], dp [i + (1 << j - 1)] [j - 1])$

注：加减的优先级比位运算的优先级高

代码：

	void rmq_init()
	{
	for(int i=1;i<=N;i++)
	dp[i][0]=arr[i];// 初始化
	for(int j=1;(1<<j)<=N;j++)
	for(int i=1;i+(1<<j)-1<=N;i++)
	dp[i][j]=min(dp[i][j-1],dp[i+(1<<j-1)][j-1]);
	}

这里需要注意一个循环变量的顺序，我们看到外层循环变量为 j，内层循环变量为 i，这是为什么呢？可以互换一下位置吗？

答案当然是不可以，我们要理解这个状态转移方程的意义，这个状态方程的含义是：先更新每两个元素中的最小值，然后通过每两个元素的最小值获得每 4 个元素中的最小值，依次类推更新所有长度的最小值。

# 查询

假设我们需要查询区间 [l ，r] 中的最小值，令 k = 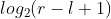，则区间 [l, r] 的最小值 RMQ [l,r] = min (dp [l] [k], dp [r - (1 << k) + 1] [k]);

dp [l][k] 维护的是区间 [l, l + 2^k - 1] , dp [r - (1 << k) + 1][k] 维护的是区间 [r - 2^k + 1, r] 。

那么只要我们保证 ≤ 就能保证 RMQ [l,r] = min (dp [l] [k], dp [r - (1 << k) + 1] [k])；

	int rmq(int l,int r)
	{
	int k=log2(r-l+1);
	return min(dp[l][k],dp[r-(1<<k)+1][k]);
	}

# 单调栈

#include <cstdio>
#include <stack>
using namespace std;
int n, a[3000003], f[3000003];

int main(void)
{
	stack<int> s;
	scanf("%d", &n);
	for (int i = 1; i <= n; i++)
	{
		scanf("%d", &a[i]);
	}

    //从后往前取数组中的元素，和栈中的元素进行比较
    //保持栈中的元素往栈顶方向递减
    //栈中保存的是元素在数组中的位置
	for (int i = n; i >= 1; i--)
	{
		while (!s.empty() && a[i] >= a[s.top()]) 
			s.pop();

		f[i] = s.empty() ? 0 : s.top();
		s.push(i);
	}

	for (int i = 1; i <= n; i++)
		printf("%d ", f[i]);

	return 0;
}

# 归并排序

	#include <stdlib.h>
	#include <stdio.h>

	void Merge(int sourceArr[],int tempArr[], int startIndex, int midIndex, int endIndex)
	{
	int i = startIndex, j=midIndex+1, k = startIndex;

	while(i!=midIndex+1 && j!=endIndex+1)
	{
	if(sourceArr[i] > sourceArr[j])
	tempArr[k++] = sourceArr[j++];
	else
	tempArr[k++] = sourceArr[i++];
	}

	while(i != midIndex+1)
	tempArr[k++] = sourceArr[i++];

	while(j != endIndex+1)
	tempArr[k++] = sourceArr[j++];

	for(i=startIndex; i<=endIndex; i++)
	sourceArr[i] = tempArr[i];
	}


	// 内部使用递归
	void MergeSort(int sourceArr[], int tempArr[], int startIndex, int endIndex)
	{
	int midIndex;
	if(startIndex < endIndex)
	{
	midIndex = startIndex + (endIndex-startIndex) / 2;// 避免溢出 int
	MergeSort(sourceArr, tempArr, startIndex, midIndex);
	MergeSort(sourceArr, tempArr, midIndex+1, endIndex);
	Merge(sourceArr, tempArr, startIndex, midIndex, endIndex);
	}
	}


	int main(int argc, char * argv[])
	{
	int a[8] = {50, 10, 20, 30, 70, 40, 80, 60};
	int i, b[8];
	MergeSort(a, b, 0, 7);
	for(i=0; i<8; i++)
	printf("%d ", a[i]);
	printf("\n");
	system("pause");
	return 0;
	}

# 快速排序

用以划分区间的元素 A [left] 被称为主元：

	// 对区间 [left, right] 进行划分
	int Partition(int A[], int left, int right)
	{
	int temp = A[left]; // 将 A [left] 存放至临时变量 temp

	while(left < right) // 只要 left 与 right 不相遇
	{
	while(left < right && temp < A[right]) // 反复左移 right
	right--;
	A[left] = A[right]; // 将 A [right] 挪到 A [left]

	while(left < right && temp >= A[left]) // 反复右移 left
	left++;

	A[right] = A[left]; // 将 A [left] 挪到 A [right]
	}
	A[left] = temp; // 把 temp 放到 left 与 right 相遇的地方
	return left; // 返回相遇的下标
	}

快速排序的思路是：

调整序列中的元素，使当前序列最左端的元素在调整后满足左侧所有元素均不超过该元素、右侧所有元素均大于该元素。
对该元素的左侧和右侧分别递归进行 1. 的调整，知道当前调整区间的长度不超过 1.

	// 快速排序，left 与 right 初值为序列首尾下标
	void quickSort(int A[], int left, int right)
	{
	if(left < right) // 当前区间的长度不超过 1
	{
	int pos = Partition(A[], left, right);
	quickSort(A[], left, pos - 1); // 对左子区间递归进行快速排序
	quickSort(A[], pos + 1, right); // 对右子区间递归进行快速排序
	}
	}

# 随机数

	#include <stdio.h>

	// 以下为需要添加的头文件
	#include <stdlib.h>
	#include <time.h>

	int main()
	{
	srand((unsigned)time(NULL)); // 生成随机数的种子
	for (int i = 0; i < 10; i++)
	printf("%d ", rand()); //rand () 为生成随机数的函数

	for (int i = 0; i < 10; i++)
	printf("%d ", rand() % 2); //[0, 1]

	for (int i = 0; i < 10; i++)
	printf("%d ", rand() % 5 + 3); //[3, 7]



	}

rand () 函数只能生成 [0, RAND_MAX] 范围内的整数（RAND_MAX 是 stdlib.h 中的一个常数，在不同系统环境中，该常数的值可能不同）。因此如果想要输出给定范围 [a, b] 内的随机数，需要使用 rand () % (b - a + 1) + a。显然 rand () % (b - a + 1) 的范围是 [0, b - a]，再加上 a 之后就是 [a, b]。

# 并查集

# 初始化

	for(int i = 1; i <= N; i++)
	{
	father[i] = i; // 令 father [i] 为 - 1 也可
	}

# 查找

规定一个集合中只存在一个根结点，因此查找操作就是对给定的结点寻找其根结点的过程。实现的方式可以是递推或递归，思路都是反复寻找父亲结点，知道找到根结点（father [x] = x）

递推

	//findFather 函数返回元素 x 所在集合的根结点
	int findFather(int x)
	{
	while(x != father[x]) // 如果不是根结点，继续循环
	{
	x = father[x]; // 获得自己父亲的根结点
	}
	return x;
	}

递归

	int findFather(int x)
	{
	if(x == father[x]) // 如果找到根结点，则返回根结点编号 x
	return x;
	else // 否则，递归判断 x 的父亲结点是否是根结点
	return findFather(father[x]);
	}

# 合并

	void Union(int a, int b)
	{
	int faA = findFather(a); // 查找 a 的根结点，即为 faA
	int faB = findFather(b); // 查找 b 的根结点，即为 faB
	if(faA != faB) // 如果不属于同一个集合
	father[faA] = faB; // 合并它们
	}

# 路径压缩

把当前查询结点的路径上的所有结点的父亲都指向根结点

转换的步骤：

按原先的写法获得 x 的根结点 r
重新从 x 开始走一遍寻找根结点的过程，把路径上经过的所有结点的父亲全部改为根结点 r

	int findFather(int x)
	{
	// 由于 x 在下面的 while 中会变成根结点，因此先把原先的 x 保存一下
	int a = x;

	// 寻找根结点
	while(x != father[x])
	x = father[x];

	// 到这里，x 存放的是根结点，下面把路径上的所有结点的 father 都改成根结点
	while(a != father[a])
	{
	int z = a; // 因为 a 要被 father [a] 覆盖，所以先保存 a 的值，以修改 father [a]
	a = father[a]; //a 回溯父亲结点
	father[z] = x; // 将原先的结点 a 的父亲改为根结点 x
	}

	return x; // 返回根结点
	}

递归写法

	int findFather(int v)
	{
	if(v == father[v]) // 找到根结点
	return v;
	else
	{
	int F = findFather(father[v]); // 递归寻找 father [v] 的根结点 F
	father[v] = F; // 将根结点 F 赋给 father [v]
	return F; // 返回根结点 F
	}
	}

# 种类并查集

一般的并查集，维护的是具有连通性、传递性的关系，例如亲戚的亲戚是亲戚。但是，有时候，我们要维护另一种关系：敌人的敌人是朋友。种类并查集就是为了解决这个问题而诞生的。

我们先来看一个例题：

（洛谷 P1525 关押罪犯）

题目描述
城现有两座监狱，一共关押着名罪犯，编号分别为。他们之间的关系自然也极不和谐。很多罪犯之间甚至积怨已久，如果客观条件具备则随时可能爆发冲突。我们用 “怨气值”（一个正整数值）来表示某两名罪犯之间的仇恨程度，怨气值越大，则这两名罪犯之间的积怨越多。如果两名怨气值为的罪犯被关押在同一监狱，他们俩之间会发生摩擦，并造成影响力为的冲突事件。
每年年末，警察局会将本年内监狱中的所有冲突事件按影响力从大到小排成一个列表，然后上报到 S 城 Z 市长那里。公务繁忙的 Z 市长只会去看列表中的第一个事件的影响力，如果影响很坏，他就会考虑撤换警察局长。
在详细考察了名罪犯间的矛盾关系后，警察局长觉得压力巨大。他准备将罪犯们在两座监狱内重新分配，以求产生的冲突事件影响力都较小，从而保住自己的乌纱帽。假设只要处于同一监狱内的某两个罪犯间有仇恨，那么他们一定会在每年的某个时候发生摩擦。
那么，应如何分配罪犯，才能使 Z 市长看到的那个冲突事件的影响力最小？这个最小值是多少？
输入格式
每行中两个数之间用一个空格隔开。第一行为两个正整数，分别表示罪犯的数目以及存在仇恨的罪犯对数。接下来的 MM 行每行为三个正整数，表示号和号罪犯之间存在仇恨，其怨气值为。数据保证，且每对罪犯组合只出现一次。
输出格式
共 1 行，为 Z 市长看到的那个冲突事件的影响力。如果本年内监狱中未发生任何冲突事件，请输出 0。

其实很容易想到，这里可以贪心，把所有矛盾关系从大到小排个序，然后尽可能地把矛盾大的犯人关到不同的监狱里，直到不能这么做为止。这看上去可以用并查集维护，但是有一个问题：我们得到的信息，不是哪些人应该在相同的监狱，而是哪些人应该在不同的监狱。这怎么处理呢？这个题其实有很多做法，但这里，我们介绍使用种类并查集的做法。

我们开一个两倍大小的并查集。例如，假如我们要维护 4 个元素的并查集，我们改为开 8 个单位的空间：

我们用 1_{4 维护 ** 朋友 ** 关系（就这道题而言，是指关在同一个监狱的狱友），用 5}8 维护敌人关系（这道题里是指关在不同监狱的仇人）。现在假如我们得到信息：1 和 2 是敌人，应该怎么办？

我们 merge(1, 2+n), merge(1+n, 2); 。这里 n 就等于 4，但我写成 n 这样更清晰。对于 1 个编号为 i 的元素，i+n 是它的敌人。所以这里的意思就是：1 是 2 的敌人，2 是 1 的敌人。

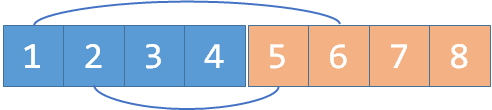
现在假如我们又知道 2 和 4 是敌人，我们 merge(2, 4+n), merge(2+n, 4); ：

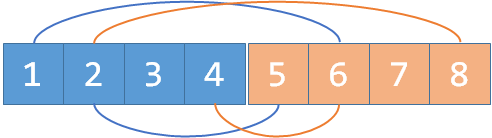
发现了吗，敌人的敌人就是朋友，2 和 4 是敌人，2 和 1 也是敌人，所以这里，1 和 4 通过 2+n 这个元素间接地连接起来了。这就是种类并查集工作的原理。

代码如下：

	#include <cstdio>
	#include <cctype>
	#include <algorithm>
	int read() // 快速读入，可忽略
	{
	int ans = 0;
	char c = getchar();
	while (!isdigit(c))
	c = getchar();
	while (isdigit(c))
	{
	ans = (ans << 3) + (ans << 1) + c - '0';
	c = getchar();
	}
	return ans;
	}
	struct data // 以结构体方式保存便于排序
	{
	int a, b, w;
	} C[100005];
	int cmp(data &a, data &b)
	{
	return a.w > b.w;
	}
	int fa[40005], rank[40005]; // 以下为并查集
	int find(int a)
	{
	return (fa[a] == a) ? a : (fa[a] = find(fa[a]));
	}
	int query(int a, int b)
	{
	return find(a) == find(b);
	}
	void merge(int a, int b)
	{
	int x = find(a), y = find(b);
	if (rank[x] >= rank[y])
	fa[y] = x;
	else
	fa[x] = y;
	if (rank[x] == rank[y] && x != y)
	rank[x]++;
	}
	void init(int n)
	{
	for (int i = 1; i <= n; ++i)
	{
	rank[i] = 1;
	fa[i] = i;
	}
	}
	int main()
	{
	int n = read(), m = read();
	init(n * 2); // 对于罪犯 i，i+n 为他的敌人
	for (int i = 0; i < m; ++i)
	{
	C[i].a = read();
	C[i].b = read();
	C[i].w = read();
	}
	std::sort(C, C + m, cmp);
	for (int i = 0; i < m; ++i)
	{
	if (query(C[i].a, C[i].b)) // 试图把两个已经被标记为 “朋友” 的人标记为 “敌人”
	{
	printf("%d\n", C[i].w); // 此时的怒气值就是最大怒气值的最小值
	break;
	}
	merge(C[i].a, C[i].b + n);
	merge(C[i].b, C[i].a + n);
	if (i == m - 1) // 如果循环结束仍无冲突，输出 0
	puts("0");
	}
	return 0;
	}

刚才我说，种类并查集可以维护敌人的敌人是朋友这样的关系，这种说法不够准确，较为本质地说，种类并查集（包括普通并查集）维护的是一种循环对称的关系。

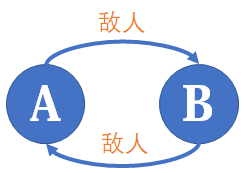
所以如果是三个及以上的集合，只要每个集合都是等价的，且集合间的每个关系都是等价的，就能够用种类并查集进行维护。例如下面这道题：

题目描述
动物王国中有三类动物 A,B,C，这三类动物的食物链构成了有趣的环形。A 吃 B，B
吃 C，C 吃 A。
现有 N 个动物，以 1 － N 编号。每个动物都是 A,B,C 中的一种，但是我们并不知道
它到底是哪一种。
有人用两种说法对这 N 个动物所构成的食物链关系进行描述：
第一种说法是 “1 X Y”，表示 X 和 Y 是同类。
第二种说法是 “2 X Y”，表示 X 吃 Y 。
此人对 N 个动物，用上述两种说法，一句接一句地说出 K 句话，这 K 句话有的是真
的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。
・当前的话与前面的某些真的话冲突，就是假话
・当前的话中 X 或 Y 比 N 大，就是假话
・当前的话表示 X 吃 X，就是假话
你的任务是根据给定的 N 和 K 句话，输出假话的总数。
输入格式
从 http://eat.in 中输入数据
第一行两个整数，N，K，表示有 N 个动物，K 句话。
第二行开始每行一句话（按照题目要求，见样例）
输出格式
输出到 eat.out 中
一行，一个整数，表示假话的总数。

我们会发现，A、B、C 三个种群天然地符合用种类并查集维护的要求。

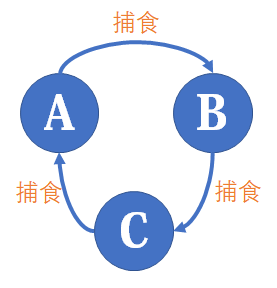
于是我们可以用一个三倍大小的并查集进行维护，用 i+n 表示 i 的捕食对象，而 i+2n 表示 i 的天敌。

	/*
	* 对于每只动物，想象它在食物链中的位置，有它的猎物还有天敌
	*
	* 我们维护三个并查集，序号分别为 1~n、n+1~2n、2n+1~3n
	*
	* 第一部分表示本身，第二部分表示猎物，第三部分表示天敌
	*
	* 每只动物在每个部分中都有一个编号，在每个部分中的意义都不一样
	* 表示捕食关系时将不同部分中的动物编号合并起来
	* 表示同类关系时将同一部分中的动物编号合并起来
	*/

	#include <iostream>
	using namespace std;

	const int N = 5e6 + 5;

	int fa[N];

	int find(int x)
	{
	if (x == fa[x])
	return x;
	else
	return fa[x] = find(fa[x]);
	}

	void uni(int x, int y)
	{
	int fax = find(x);
	int fay = find(y);

	fa[fax] = fay;
	}

	int main()
	{
	ios::sync_with_stdio(false);
	cin.tie(0);
	int n, k; //n 个动物，k 句话
	cin >> n >> k;
	int x, y;

	// 初始化
	for (int i = 1; i <= 3 * n; i++)
	{
	fa[i] = i;
	}

	int ans = 0;
	int opt;
	for (int i = 1; i <= k; i++)
	{
	cin >> opt >> x >> y;

	if (x > n \|\| y > n)
	{
	ans++;
	continue;
	}

	if (opt == 1)
	{
	/*
	* 判断 x 和 y 是否是同类，不是通过判断两者是否在同一个并查集中
	* 因为如果 x 和 y 如果满足捕食关系的话，两个不在同一个并查集中
	* 此时不能把 x 和 y 视为同类
	*
	* 所以通过判断 x 和 y 是否满足捕食关系来判断两者是否是同类
	*/
	if (find(x) == find(y + n) \|\| find(x) == find(y + 2 * n))
	{
	ans++;
	continue;
	}
	else
	{
	uni(x, y);
	uni(x + n, y + n);
	uni(x + 2 * n, y + 2 * n);
	}
	}
	else if (opt == 2)
	{
	if (find(x) == find(y) \|\| find(x) == find(y + 2 * n) \|\| x == y)
	{
	ans++;
	continue;
	}
	else
	{
	uni(x, y + n);
	uni(x + n, y + 2 * n);
	uni(x + 2 * n, y);
	}
	}
	}
	cout << ans;
	}

# 最小生成树

###kruskal 算法

	#include <stdio.h>
	#include <algorithm>
	using namespace std;
	const int MAXV = 110;
	const int MAXE = 10010;

	// 边集定义部分
	struct edge {
	int u, v; // 边的两个端点编号
	int cost; // 边权
	}E[MAXE]; // 最多有 MAXE 条边

	bool cmp(edge a, edge b)
	{
	return a.cost < b.cost;
	}

	// 并查集部分
	int father[MAXV]; // 并查集数组

	// 并查集查询函数
	int findFather(int x)
	{
	int a = x;

	while (x != father[x])
	x = father[x];

	// 路径压缩
	while (a != father[a])
	{
	int z = a;
	a = father[a];
	father[z] = x;
	}

	return x;
	}

	//kruskal 部分，返回最小生成树的边权之和，参数 n 为顶点个数，m 为图的边数
	int kruskal(int n, int m)
	{
	//ans 为所求边权之和，Num_Edge 为当前生成树的边数
	int ans = 0, Num_Edge = 0;

	for (int i = 0; i < n; i++) // 顶点范围是 [0, n-1]
	{
	father[i] = i;// 并查集初始化
	}

	sort(E, E + m, cmp); // 所有边按边权从小到大排序

	for (int i = 0; i < m; i++) // 枚举所有边
	{
	int faU = findFather(E[i].u); // 查询测试边两个端点所在集合的根结点
	int faV = findFather(E[i].v);
	if (faU != faV) // 如果不在一个集合中
	{
	father[faU] = faV; // 合并集合（即把测试边加入最小生成树中）
	ans += E[i].cost; // 边权之和增加测试边的边权
	Num_Edge++; // 当前生成树的边数加 1
	if (Num_Edge == n - 1)
	break; // 边数等于顶点数减 1 时结束算法

	}
	}

	if (Num_Edge != n - 1)
	return -1; // 无法连通时返回 - 1
	else
	return ans; // 返回最小生成树的边权之和
	}

	int main(void)
	{
	int n, m;
	scanf("%d %d", &n, &m); // 顶点数、边数
	for (int i = 0; i < m; i++)
	{
	scanf("%d %d %d", &E[i].u, &E[i].v, &E[i].cost); // 两个端点编号、边权
	}

	int ans = kruskal(n, m); //kruskal 算法入口
	printf("%d", ans);

	return 0;
	}

# prim 算法

	#include <stdio.h>
	#include <algorithm>
	using namespace std;
	const int MAXV = 1000; // 最大顶点数
	const int INF = 1000000000; // 设 INF 为一个很大的数

	int n, m, G[MAXV][MAXV]; //n 为顶点数，
	int d[MAXV]; // 顶点与集合 S 的最短距离
	bool vis[MAXV] = { false }; // 标记数组，vis [i] == true 表示已访问，初值均为 false

	int prim() // 默认 0 号为初始点，函数返回最小生成树的边权之和
	{
	fill(d, d + MAXV, INF); //fill 函数将整个 d 数组赋值为 INF
	d[0] = 0; // 只有 0 号顶点到集合 S 的距离为 0，其余全为 INF
	int ans = 0; // 存放最小生成树的边权之和

	for (int i = 0; i < n; i++) // 循环 n 次
	{
	int u = -1, MIN = INF; //u 使 d [u] 最小，MIN 存放最小的 d [u]

	for (int j = 0; j < n; j++) // 找到未访问的顶点中的 d [] 最小的
	{
	if (vis[j] == false && d[j] < MIN)
	{
	u = j;
	MIN = d[j];
	}
	}

	// 找不到小于 INF 的 d [u]，则剩下的顶点和集合 S 不连通
	if (u == -1)
	return -1;

	vis[u] = true; // 标记 u 为已访问

	ans += d[u]; // 将与集合 S 距离最小的边加入最小生成树

	for (int v = 0; v < n; v++)
	{
	//v 未访问 && u 能到达 v && 以 u 为中介点可以使 v 离集合 S 更近
	if (vis[v] == false && G[u][v] != INF && G[u][v] < d[v])
	{
	d[v] = G[u][v]; // 将 G [u][v] 赋值给 d [v]
	}
	}


	}
	return ans; // 返回最小生成树的边权之和

	}

	int main(void)
	{
	int u, v, w;
	scanf("%d %d", &n, &m); // 顶点个数、边数
	fill(G[0], G[0] + MAXV * MAXV, INF); // 初始化图 G

	for (int i = 0; i < m; i++)
	{
	scanf("%d %d %d", &u, &v, &w); // 输入 u、v 以及边权
	G[u][v] = G[v][u] = w; // 无向图
	}

	int ans = prim(); //prim 算法入口
	printf("%d", ans);
	return 0;
	}

# 链式前向星

	我们建立边结构体为:

	struct Edge

	{
	int next;
	int to;
	int w;
	}edge[MAXE];
	其中：
	edge[i].to表示第i条边的终点,
	edge[i].next表示与第i条边同起点的下一条边的存储位置,
	edge[i].w为边权值.

另外还有一个数组 head []，head [i] 用来表示以 i 为起点的第一条边存储的位置，实际上你会发现这里的第一条边存储的位置其实在以 i 为起点的所有边的最后输入的那个编号

head [] 数组一般初始化为 - 1

	void add_edge(int u, int v, int w){ // 加边函数。u 为起点，v 为终点，w 为边权

	edge[cnt].to=v; // 终点

	edge[cnt].w=w; // 权值

	edge[cnt].next=head[u]; // 以 u 为起点的最后一条边的编号

	head[u]=cnt++; // 更新以 u 为起点的上一条边的编号

	}

在这里进行边的衔接的时候颇似栈，next 更像是 last（上一个）

	给你一组数据：
	第一行表示 5 个顶点 7 条边
	接下来是7条边的起点、终点和权值

	5 7
	1 2 1
	2 3 2
	3 4 3
	1 3 4
	4 1 5
	1 5 6
	4 5 7

	依据next，head数组的约定，并按边的输入顺序从0开始对边进行编号，
	然后按照上面的数据就可以写出下面的过程：

	对于1 2 1这条边：edge[0].to=2; edge[0].next=-1; head[1]=0;

	对于2 3 2这条边：edge[1].to=3; edge[1].next=-1; head[2]=1;

	对于3 4 3这条边：edge[2].to=4; edge[2],next=-1; head[3]=2;

	对于1 3 4这条边：edge[3].to=3; edge[3].next= 0; head[1]=3;

	对于4 1 5这条边：edge[4].to=1; edge[4].next=-1; head[4]=4;

	对于1 5 6这条边：edge[5].to=5; edge[5].next= 3; head[1]=5;

	对于4 5 7这条边：edge[6].to=5; edge[6].next= 4; head[4]=6;

	很明显,head[i]保存的是以i为起点的所有边中编号最大的那个,而把这个当作顶点i的第一条起始边的位置.

注：边数组从 0 开始计数，顶点编号从 1 开始

	遍历函数如下：
	for(int i=1; i<=n; i++){ //n 个起点
	cout<<i<<endl;
	for(int j=head[i]; j!=-1; j=edge[j].next) // 遍历以 i 为起点的所有边
	cout<<i<<" "<<edge[j].to<<" "<<edge[j].w<<endl;
	cout<<endl;
	}

	第一层for循环：依次遍历以1...n为起点的边的集合。
	第二层for循环：遍历以i为起点的所有边，j首先等于head[i]。
	注意：head[i]表示与点i起点相同的最后一条边的编号。
	然后，通过edge[j].next来找与边j起点相同的上一条边的编号，终止条件为edge[j].next=-1。

总结性代码

	#include<bits/stdc++.h>
	using namespace std;
	const int maxn = 1005;// 点数最大值
	int n, m, cnt;//n 个点，m 条边
	struct Edge
	{
	int to, w, next;// 终点，边权，同起点的上一条边的编号
	}edge[maxn];// 边集
	int head[maxn];//head [i], 表示以 i 为起点的第一条边在边集数组的位置（编号）
	void init()// 初始化
	{
	for (int i = 0; i <= n; i++) head[i] = -1;
	cnt = 0;
	}
	void add_edge(int u, int v, int w)// 加边，u 起点，v 终点，w 边权
	{
	edge[cnt].to = v; // 终点
	edge[cnt].w = w; // 权值
	edge[cnt].next = head[u];// 以 u 为起点上一条边的编号，也就是与这个边起点相同的上一条边的编号
	head[u] = cnt++;// 更新以 u 为起点上一条边的编号
	}
	int main()
	{
	cin >> n >> m;
	int u, v, w;
	init();// 初始化
	for (int i = 1; i <= m; i++)// 输入 m 条边
	{
	cin >> u >> v >> w;
	add_edge(u, v, w);// 加边
	/*
	加双向边
	add_edge (u, v, w);
	add_edge (v, u, w);
	*/
	}
	for (int i = 1; i <= n; i++)//n 个起点
	{
	cout << i << endl;
	for (int j = head[i]; j != -1; j = edge[j].next)// 遍历以 i 为起点的边
	{
	cout << i << " " << edge[j].to << " " << edge[j].w << endl;
	}
	cout << endl;
	}
	return 0;
	}
	【测试样例】

	in：

	5 7
	1 2 1
	2 3 2
	3 4 3
	1 3 4
	4 1 5
	1 5 6
	4 5 7

	out：

	1 // 以 1 为起点的边的集合
	1 5 6
	1 3 4
	1 2 1

	2 // 以 2 为起点的边的集合

	2 3 2

	3 // 以 3 为起点的边的集合
	3 4 3

	4 // 以 4 为起点的边的集合
	4 5 7
	4 1 5

	5 // 以 5 为起点的边不存在

# 单调队列

# 进制哈希

# 最短路径

# Dijkstra 算法

#### 堆优化

堆优化即使用 stl 的优先队列，优先队列就是用堆存储的

	// 洛谷 P4779
	#include <iostream>
	#include <queue>
	#include <algorithm>
	using namespace std;

	const int maxn = 100005;
	const int maxm = 200005;
	const int INF = 0x3fffffff;

	// 链式前向星部分
	int cnt, head[maxn];

	struct edge {
	int to;
	int dis;
	int next;
	}e[maxm];

	void add(int u, int v, int dis)
	{
	cnt++;
	e[cnt].to = v;
	e[cnt].dis = dis;
	e[cnt].next = head[u];
	head[u] = cnt;
	}

	// 图的相关结构部分
	struct node {
	int to;
	int dis;
	node(int _to, int _dis) : to(_to), dis(_dis) {}
	friend bool operator < (node a, node b)
	{
	return a.dis > b.dis;
	}
	};

	bool vis[maxn]; // 访问数组
	int d[maxn]; // 距离数组
	int n, m, s; //n 个点，m 条有向边，起点为 s

	void dijkstra(int s)
	{
	priority_queue<node> q;
	fill(d + 1, d + maxn, INF);
	d[s] = 0;
	q.push(node(s, 0));

	while (!q.empty())
	{
	node tmp = q.top();
	q.pop();
	if (vis[tmp.to])
	continue;

	vis[tmp.to] = true;
	d[tmp.to] = tmp.dis;
	for (int i = head[tmp.to]; i; i = e[i].next)
	{
	int v = e[i].to;
	int dis = e[i].dis;
	if (vis[v] == false && d[v] > d[tmp.to] + dis)
	{
	d[v] = d[tmp.to] + dis;
	q.push(node(v, d[v]));
	}
	}

	}
	}

	int main()
	{
	cin >> n >> m >> s;
	int u, v, w;
	for (int i = 1; i <= m; i++)
	{
	cin >> u >> v >> w;
	add(u, v, w);
	}

	dijkstra(s);
	for (int i = 1; i <= n; i++)
	{
	cout << d[i] << " ";
	}
	}

#### 普通版

邻接表

	struct Node{
	int v, dis; //v 为边的目标顶点，dis 为边权
	};

	vector<Node> Adj[MAXV]; // 图 G，Adj [u] 存放从顶点 u 出发可以到达的所有顶点
	int d[MAXV]; //n 为顶点数，图 G 使用邻接表实现，MAXV 为最大顶点数
	int n;
	int d[MAXV]; // 起点到达各点的最短路径长度
	bool vis[MAXV] = {false}; // 标记数组

	void Dijkstra(int s)
	{
	fill(d, d + MAXV, INF);

	for(int i = 0; i < n; i++)
	{
	int u = -1;
	int MIN = INF;
	for(int j = 0; j < n; j++)
	{
	if(vis[j] == false && d[j] < MIN)
	{
	u = j;
	MIN = d[j];
	}
	}

	if(u == -1)
	return;
	vis[u] = true;

	for(int j = 0; j < Adj[u].size(); j++)
	{
	int v = Adj[u][j].v;
	int dis = Adj[u][j].dis;
	if(vis[v] == false && d[u] + dis < d[v])
	d[v] = d[u] + dis;
	}
	}
	}

以下为邻接矩阵

	#include <stdio.h>
	#include <algorithm>
	using namespace std;

	int n, m, s; //n 为顶点数，m 为边数， s 为起点
	const int INF = 1000000000; // 设 INF 是一个很大的数
	const int MAXV = 1000; // 最大顶点数
	int d[MAXV];
	int G[MAXV][MAXV];
	bool vis[MAXV] = {false}; // 标记数组，vis [i] == true 表示已访问。初值均为 false

	void Dijkstra(int s) //s 为起点
	{
	fill(d, d + MAXV, INF);

	d[s] = 0; // 起点 s 到达自身的距离为 0

	for(int i = 0; i < n; i++) // 循环 n 次
	{
	int u = -1;
	int MIN = INF; //u 使 d [u] 最小，MIN 存放该最小的 d [u]
	for(int j = 0; j < n; j++) // 找到未访问的顶点中 d [] 最小的
	{
	if(vis[j] == false && d[j] < MIN)
	{
	u = j;
	MIN = d[j];
	}
	}

	// 找不到小于 INF 的 d [u]，说明剩下的顶点和起点 s 不连通
	if(u == -1)
	return;

	vis[u] = true; // 标记 u 为已访问

	for(int v = 0; v < n; v++) // 遍历所有的顶点
	{
	// 如果 v 未访问 && u 能到达 v && 以 u 为中介点可以使 f [v] 更优
	if(!vis[v] && G[u][v] != INF && d[u] + G[u][v] < d[v])
	d[v] = d[u] + G[u][v]; // 优化 d [v]
	}
	}

	}

	int main()
	{
	int u, v, w;
	scanf("%d%d%d", &n, &m, &s); // 顶点个数、边数、起点编号
	fill(G[0], G[0] + MAXV * MAXV, INF); // 初始化图 G

	for(int i = 0; i < m; i++)
	{
	scanf("%d%d%d", &u, &v, &w); // 输入 u，v 以及 u->v 的边权
	G[u][v] = w;
	}

	Dijkstra(s); //Dijkstra 算法入口

	for(int i = 0; i < n; i++)
	printf("%d ", d[i]); // 输出所有顶点的最短距离

	return 0;
	}

上面的算法中提到的 “以 u 为中介点可以使起点 s 到顶点 v 的最短距离 d [v] 更优” 隐含了：使 d [v] 变得更小的方案是让 u 作为从 s 到 v 的最短路径上 v 的前一个结点。不妨把这个信息记录下来，设置一个数组 pre []。令 pre [v] 表示从起点 s 到顶点 v 的最短路径 v 的前一个顶点（即前驱结点）的编号。

伪代码增加处：

	if(如果v未访问 && u能到达v && 以u为中介点可以使f[v]更优)
	{
	优化d[v];
	令u的前驱为u;
	}

具体实现中：

	#include <stdio.h>
	#include <algorithm>
	using namespace std;

	int n, m, s; //n 为顶点数，m 为边数， s 为起点
	const int INF = 1000000000; // 设 INF 是一个很大的数
	const int MAXV = 1000; // 最大顶点数
	int d[MAXV];
	int G[MAXV][MAXV];
	bool vis[MAXV] = {false}; // 标记数组，vis [i] == true 表示已访问。初值均为 false
	int pre[MAXV]; //pre [v] 表示从起点到顶点 v 的最短路径上 v 的前一个顶点（新添加）

	void Dijkstra(int s) //s 为起点
	{
	fill(d, d + MAXV, INF);
	for(int i = 0; i < n; i++)
	pre[i] = i; // 初始状态设每个点的前驱为自身（新添加）
	d[s] = 0; // 起点 s 到达自身的距离为 0

	for(int i = 0; i < n; i++) // 循环 n 次
	{
	int u = -1;
	int MIN = INF; //u 使 d [u] 最小，MIN 存放该最小的 d [u]
	for(int j = 0; j < n; j++) // 找到未访问的顶点中 d [] 最小的
	{
	if(vis[j] == false && d[j] < MIN)
	{
	u = j;
	MIN = d[j];
	}
	}

	// 找不到小于 INF 的 d [u]，说明剩下的顶点和起点 s 不连通
	if(u == -1)
	return;

	vis[u] = true; // 标记 u 为已访问

	for(int v = 0; v < n; v++) // 遍历所有的顶点
	{
	// 如果 v 未访问 && u 能到达 v && 以 u 为中介点可以使 f [v] 更优
	if(!vis[v] && G[u][v] != INF && d[u] + G[u][v] < d[v])
	{
	d[v] = d[u] + G[u][v]; // 优化 d [v]
	pre[v] = u; // 记录 v 的前驱顶点是 u（新添加）
	}
	}
	}

	}

求整条路径

	void DFS(int s, int v)
	{
	if(s == v)
	{
	printf("%d ", s);
	return;
	}

	DFS(s, pre[v]);
	printf("%d ", v);

	}

# 新增边权

cost [u] [v] 表示 u->v 的花费（从题目输入），增加一个数组 c []，令从起点 s 到达顶点 u 的最少花费为 c [u]，初始化时只有 c [s] 为 0、其余为 INF。

	for(int v = 0; v < n; v++)
	{
	// 如果 v 未访问 && u 能到达 v
	if(vis[v] == false && G[u][v] != INF)
	{
	if(d[u] + G[u][v] < d[v]) // 以 u 为中介点可以使 d [v] 更优
	{
	d[v] = d[u] + G[u][v];
	c[v] = c[u] + cost[u][v];
	}
	else if(d[u] + G[u][v] == d[v] && c[u] + cost[u][v] < c[v])
	c[v] = c[u] + cost[u][v]; // 最短距离相同时看能够使 c [v] 更优
	}
	}

# 新增点权

用 weight [u] 表示城市 u 中的物资数目（由题目输入），并增加一个数组 w []，令从起点到达顶点 u 可以收集到的最大物资为 w [u]，初始化时只有 w [s] 为 weight [s]、其余 w [u] 均为 0.

	for(int v = 0; v < n; v++)
	{
	if(vis[v] == false && G[u][v] != INF)
	{
	if(d[u] + G[u][v] < d[v])
	{
	d[v] = d[u] + G[u][v];
	w[v] = w[u] + weight[v];
	}
	else if(d[u] + G[u][v] == d[v] && w[u] + weight[v] > w[v])
	w[v] = w[u] + weight[v]; // 最短距离相同时看能否使 w [v] 更优
	}
	}

# 最短路径条数

增加一个数组 num[] ，令从起点 s 到达顶点 u 的最短路径条数为 num[u] ，初始化时只有 num [s] 为 1、其余均为 0。

	for(int v = 0; v < n; v++)
	{
	if(vis[v] == false && G[u][v] != INF)
	{
	if(d[v] > d[u] + G[u][v])
	{
	d[v] = d[u] + G[u][v];
	num[v] = num[u];
	}
	else if(d[v] == d[u] + G[u][v])
	num[v] += num[u]; // 最短距离相同时累加 num
	}
	}

	/*
	*
	* 由于本题中图的边权为 1，则可以使用 BFS 算法结合深度来解决
	*
	* 如果某结点的相邻结点未访问过，则该相邻结点的最短路等于该结点
	* 如果某结点的相邻结点已经访问过且深度大 1，则该相邻结点的最短路加上该结点的最短路
	*
	*/

	#include <iostream>
	#include <queue>
	using namespace std;

	const int maxn = 1000005;
	const int mod = 100003;

	vector<int> Adj[maxn]; // 邻接表存储图
	int num[maxn]; // 到每一个点的最短路
	int depth[maxn]; // 每个点的深度值
	int N, M; // 图的顶点数和边数
	bool vis[maxn]; // 访问数组

	int main()
	{
	cin >> N >> M;// 顶点数和边数

	int x, y;
	for (int i = 0; i < M; i++)
	{

	cin >> x >> y;
	Adj[x].push_back(y);
	Adj[y].push_back(x); // 无向无权图
	}

	// 初始化
	num[1] = 1;
	depth[1] = 1;
	vis[1] = true;
	queue<int> q;
	q.push(1);

	while (!q.empty())
	{
	int u = q.front();
	q.pop();

	for (int i = 0; i < Adj[u].size(); i++)
	{
	int v = Adj[u][i];
	if (vis[v] == false) // 未访问过
	{
	num[v] = num[u];
	depth[v] = depth[u] + 1;
	vis[v] = true;
	q.push(v);
	}
	else // 已经访问过，其子结点已经处理过，所以不必要再入队
	{
	if (depth[v] == depth[u] + 1) // 深度相差 1
	{
	num[v] = (num[u] + num[v]) % mod;
	}
	}
	}
	}

	for (int i = 1; i <= N; i++)
	cout << num[i] << endl;
	}

# Dijkstra + DFS

先在 Dijkstra 算法中记录下所有最短路径（只考虑距离），然后从这些最短路径中选出一条第二标尺最优的路径

####Dijkstra

对需要查询某个顶点 u 是否在顶点 v 的前驱中的题目，也可以把 pre 数组设置为 set<int> 数组，此时使用 pre [v].count (u) 来查询比较方便

	vector<int> pre[MAXV];

	void Dijkstra(int s)
	{
	fill(d, d + MAXV, INF);
	d[s] = 0;
	for(int i = 0; i < n; i++) // 循环 n 次
	{
	int u = -1;
	int MIN = INF; //u 使 d [u] 最小，MIN 存放该最小的 d [u]
	for(int j = 0; j < n; j++) // 找到未访问的顶点中 d [] 最小的
	{
	if(vis[j] == false && d[j] < MIN)
	{
	u = j;
	MIN = d[j];
	}
	}

	// 找不到小于 INF 的 d [u]，说明剩下的顶点和起点 s 不连通
	if(u == -1)
	return;

	vis[u] = true; // 标记 u 为已访问

	for(int v = 0; v < n; v++) // 遍历所有的顶点
	{
	if(vis[v] == false && G[u][v] != INF)
	{
	if(d[u] + G[u][v] < d[v])
	{
	d[v] = d[u] + G[u][v]; // 优化 d [v]
	pre[v].clear(); // 清空 pre [v]
	pre[v].push_back(u); // 令 v 的前驱为 u
	}
	else if(d[u] + G[u][v] == d[v])
	pre[v].push_back(u); // 令 v 的前驱为 u
	}
	}
	}
	}

# DFS

作为全局变量的第二标尺最优值 optValue
记录最优路径的数组 path（使用 vector 来存储）
临时记录 DFS 遍历到叶子结点时的路径 tempPath（vector 存储）

	vector<int> pre[MAxv]; // 存放结点的前驱结点
	vector<int> path, tempPath; // 最优路径、临时路径
	int optValue; // 第二标尺最优值

	void DFS(int v) //v 为当前访问结点
	{
	// 递归边界
	if(v == st) // 如果到达了叶子结点 st（即路径的起点）
	{
	tempPath.push_back(v); // 将起点加入临时路径 tempPath 的最后面

	int value; // 存放临时路径 tempPath 的第二标尺的值
	计算路径tempPath上的value值
	if(value 优于 optValue)
	{
	optValue = value; // 更新第二标尺最优值与最优路径
	path = tempValue;
	}
	tempPath.pop_back();
	return;
	}

	// 递归式
	tempPath.push_back(v); // 将当前访问结点加入临时路径 tempPath 的最后面

	for(int i = 0; i < pre[v].size(); i++)
	{
	DFS(pre[v][i]); // 结点 v 的前驱结点 pre [v][i]，递归
	}

	tempPath.pop_back(); // 遍历完所有前驱结点，将当前结点 v 删除
	}

存放在 tempPath 中的路径结点是逆序的，因此访问结点需要倒着进行

	// 边权之和
	int value = 0;
	for(int i = tempPath.size()-1; i > 0; i--) // 倒着访问结点，循环条件为 i>0
	{
	// 当前结点 id，下一个结点 idNext
	int id = tempPath[i], idNext = tempPath[i-1];
	value += V[id][idNext];
	}

	// 点权之和
	int value = 0;
	for(int i = tempPath.size() - 1; i >= 0; i--) // 倒着访问结点，循环条件为 i>=0
	{
	int id = tempPath[i];
	value += W[id]; //value 增加结点 id 的点权
	}

# BF 算法

初始状态下 d [s] 为 0，因此在接下来的步骤中 d [s] 不会被改变（也就是说，最短路径树中第一层结点的 d 值被确定）。接着，通过 Bellman-Ford 算法的第一轮操作之后，最短路径树中的第二层顶点的 d 值也会被确定下来。这样计算知道最后一层顶点的 d 值确定。

	struct Node{
	int v;
	int dis; //v 为邻接边的目标顶点，dis 为邻接边的边权
	};

	vector<Node> Adj[MAXV]; // 图 G 的邻接表

	int n; //n 为顶点数，MAXV 为最大顶点数
	int d[MAXV]; // 起点到达各点的最短路径长度

	bool Bellman(int s) //s 为源点
	{
	fill(d, d + MAXV, INF); //fill 函数将整个 d 数组赋为 INF
	d[s] = 0; // 起点到达自身的距离为 0

	// 以下为求解数组 d 的部分
	for(int i = 0; i < n - 1; i++) // 执行 n-1 轮操作，n 为顶点数
	{
	for(int u = 0; u < n; u++) // 每轮操作都遍历所有的边
	{
	for(int j = 0; j < Adj[u].size(); j++)
	{
	int v = Adj[u][j].v; // 邻接边的顶点
	int dis = Adj[u][j].dis; // 邻接边的边权
	if(d[u] + dis < d[v]) // 以 u 为中介点可以使 d [v] 更小
	{
	d[v] = d[u] + dis; // 松弛操作
	}
	}
	}
	}

	// 以下为判断负环的代码
	for(int u = 0; u < n; u++) // 对每条边进行判断
	{
	for(int j = 0; j < Adj[u].size(); j++)
	{
	int v = Adj[u][j].v; // 邻接边的顶点
	int dis = Adj[u][j].dis; // 邻接边的边权
	if(d[u] + dis < d[v]) // 如果仍可以被松弛
	return false; // 说明图中有从源点可达的负环
	}
	}

	return true; // 数组 d 的所有值都已经达到最优
	}

BF 算法需要遍历所有边，显然使用邻接表会比较方便。

注意到，如果在某一轮操作中，发现所有边都没有被松弛，那么说明数组 d 中的所有值都已经达到最优，不需要再继续，提前退出即可。

负环绕一圈（经过所有顶点）后的权值之和仍为负值的环，这样会更改 d [s] 的值，引发错误。

** 需要注意的是统计最短路径条数的做法：** 由于 bellman-ford 算法期间会多次访问曾经访问过的顶点，如果单纯按照 Dijkstra 算法中介绍的 num 数组的写法，将会反复累计已经计算过的顶点。为了解决这个问题，当遇到一条和已有最短路径长度相同的路径时，必须重新计算路径条数。

	#include <stdio.h>
	#include <set>
	#include <algorithm>
	#include <vector>
	using namespace std;
	const int MAXV = 510;
	const int INF = 0x3fffffff;

	struct Node{
	int v, dis; //v 为邻接边的目标顶点，dis 为邻接边的边权
	Node (int _v, int _dis): v(_v), dis(_dis) {} // 构造函数
	};

	//n 为顶点数，m 为边数，st 和 ed 分别为起点和终点，weight [] 记录点权
	int n, m, st, ed, weight[MAXV];
	vector<int> Adj[MAXV]; // 图 G 的邻接表
	//d [] 记录最短距离，w [] 记录最大点权之和，num [] 记录最短路径条数
	int d[MAXV], w[MAXV], num[MAXV];
	set<int> pre[MAXV]; // 前驱

	void bellman(int s) //s 为源点
	{
	fill(d, d + MAXV, INF);
	memset(num, 0, sizeof(num));
	memset(w, 0, sizeof(w));
	d[s] = 0;
	w[s] = weight[s];
	num[s] = 1;

	// 以下为求解数组 d 的部分
	for(int i = 0; i < n - 1; i++)
	{
	for(u = 0; u < n; u++)
	{
	for(int j = 0; j < Adj[u].size(); j++)
	{
	int v = Adj[u][j].v;
	int dis = Adj[u][j].dis;
	if(d[u] + dis < d[v])
	{
	d[v] = d[u] + dis;
	num[v] = num[u];
	w[v] = w[u] + weight[v];
	pre[v].clear();
	pre[v].insert(u);
	}
	else if(d[u] + dis == d[v])
	{
	if(w[v] < w[u] + weight[v])
	w[v] = w[u] + weight[v];

	pre[v].insert(u);

	num[v] = 0; // 重新统计 num [v]

	for(set<int>::iterator it = pre[v].begin(); it != pre[v].end(); it++)
	num[v] += num[*it];
	}
	}
	}
	}
	}

	int main(void)
	{
	scanf("%d%d%d", &n, &m, &st, &ed);
	for(int i = 0; i < n; i++)
	scanf("%d", &weight[i]); // 读入点权

	int u, v, wt;

	for(int i = 0; i < m; i++)
	{
	scanf("%d%d%d", &u, &v, &wt);
	Adj[u].push_back(Node(v, wt));
	Adj[v].push_back(Node(u, wt));
	}

	Bellman(st);

	printf("%d %d\n", num[ed], w[ed]); // 最短距离条数，最短路径中的最大点权

	return 0;
	}

# spfa

只有当某个顶点 u 的 d [u] 值改变时，从它出发的边的邻接点 v 的 d [v] 值才有可能被改变

	vector<Node> Adj[MAXV]; // 图 G 的邻接表
	int n, d[MAXV], num[MAXV]; //num 数组记录顶点的入队次数
	bool inq[MAXV]; // 顶点是否在队列中


	bool spfa(int s)
	{
	// 初始化部分
	fill(d, d + MAXV, INF);
	memset(inq, false, sizeof(inq));
	memset(num, 0, sizeof(num));

	// 源点入队部分
	d[s] = 0;
	inq[s] = true;
	num[s]++;
	queue<int> Q;
	Q.push(s); // 源点入队

	// 主体部分
	while(!Q.empty())
	{
	int u = Q.front(); // 队首顶点编号为 u
	Q.pop(); // 出队
	inq[u] = false; // 设置 u 为不在队列中

	// 遍历 u 的所有邻接边
	for(int j = 0; j < Adj[u].size(); j++)
	{
	int v = Adj[u][j].v;
	int dis = Adj[u][j].dis;
	if(d[v] < d[u] + dis)
	{
	d[v] = d[u] + dis;
	if(inq[v] == false) // 如果 v 不在队列中
	{
	Q.push(v);
	inq[v] = true;
	num[v]++;

	if(num[v] >= n) // 有可达负环
	return false;
	}
	}
	}
	}
	return true;
	}

# Floyd 算法

解决全源最短路问题，时间复杂度为 O (n³)，决定了顶点数在 200 以内，因此应使用邻接矩阵。

	#include <stdio.h>
	#include <iostream>
	#include <algorithm>
	using namespace std;

	const int MAXV = 200; //200 为最大顶点数
	const int INF = 1000000000;
	int dis[MAXV][MAXV]; //dis [i][j] 表示顶点 i 和顶点 j 的最短距离
	int n, m; //n 为顶点数，m 为边数

	void Floyd()
	{
	for (int k = 0; k < n; k++)
	{
	for (int i = 0; i < n; i++)
	{
	for (int j = 0; j < n; j++)
	{
	if (dis[i][k] != INF && dis[k][j] != INF && dis[i][k] + dis[k][j] < dis[i][j])
	dis[i][j] = dis[i][k] + dis[k][j]; // 找到最短的路径
	}
	}
	}
	}

	int main(void)
	{
	fill(dis[0], dis[0] + MAXV, INF); //dis 数组赋初值

	cin >> n >> m;

	for (int i = 0; i < n; i++)
	dis[i][i] = 0; // 顶点 i 到顶点 i 的距离初始化为 0

	int u, v, w;
	for (int i = 0; i < m; i++)
	{
	cin >> u >> v >> w;
	dis[u][v] = w;
	}
	Floyd();

	// 输出 dis 数组
	for (int i = 0; i < n; i++)
	{
	for (int j = 0; j < n; j++)
	cout << dis[i][j] << " ";
	cout << endl;
	}

	return 0;
	}

基本思想：最开始只允许经过 1 号顶点进行中转，接下来只允许经过 1 和 2 号顶点进行中转…… 允许经过 1~n 号所有顶点进行中转，求任意两点之间的最短路程。用一句话概括就是：从 i 号顶点到 j 号顶点只经过前 k 号顶点的最短路程。

Floyd 算法就是一个利用其他点进行中转来求最短路的步骤。

# DFS 和 BFS

# DFS

邻接矩阵

	const int MAXV = 1000; // 最大顶点数
	const int INF = 1000000000; // 设 INF 为一个很大的数

	int n, G[MAXV][MAXV]; //n 为顶点数，MAXV 为最大顶点数
	bool vis[MAXV] = {false}; // 如果顶点 i 已被访问，则 vis [i]==true。初值为 false

	void DFS(int u, int depth) //u 为当前访问的顶点标号，depth 为深度
	{
	vis[u] = true; // 设置 u 已被访问
	// 如果需要对 u 进行一些操作，可以在这里进行
	// 下面对所有从 u 出发能到达的分支顶点进行枚举
	for(int v = 0; v < n; v++) // 对每个顶点 v
	{
	//v 未被访问 && u 可到达 v
	if(vis[v] == false && G[u][v] != INF)
	{
	DFS(v, depth + 1); // 访问 v，深度加 1
	}
	}
	}

	void DFSTrave() // 遍历图 G
	{
	for(int u = 0; u < n; u++) // 对每个顶点 u
	{
	if(vis[u] == false) // 如果 u 未被访问
	DFS(u, 1); // 访问 u 和 u 所在的连通块，1 表示初始为第一层
	}
	}

邻接表

	const int MAXV = 1000; // 最大顶点数
	const int INF = 1000000000; // 设 INF 为一个很大的数

	bool vis[MAXV] = {false}; // 如果顶点 i 已被访问，则 vis [i]==true。初值为 false
	vector<int> Adj[MAXV]; // 图 G 的邻接表
	int n; //n 为顶点数，MAXV 为最大顶点数

	void DFS(int u, int depth)
	{
	vis[u] = true;

	for(int j = 0; j < Adj[u].size(); j++)
	{
	int v = Adj[u][j];
	if(vis[v] == false)
	DFS(v, depth + 1);
	}
	}

	void DFSTrave()
	{
	for(int u = 0; u < n; u++)
	{
	if(vis[u] == false)
	DFS(u, 1);
	}
	}

# BFS

#### 邻接矩阵

	int n, G[MAXV][MAXV]; //n 为顶点数，MAXV 为最大顶点数
	bool inq[MAXV] = {false}; // 若顶点 i 曾入过队列（也即访问过），则 inq [i]==true。初值为 false

	void BFS(int u) // 遍历 u 所在的连通块
	{
	queue<int> q; // 定义队列 q
	inq[u] = true; // 设置 u 已被加入过队列
	q.push(u); // 将初始点 u 入队

	while(!q.empty()) // 只要队列非空
	{
	int v = q.front(); // 取出队首元素
	q.pop(); // 将队首元素出队

	for(int j = 0; j < n; j++)
	{
	// 如果 u 的邻接点 v 未曾加入过队列
	if(vis[j] == false && G[v][j] != INF)
	{
	vis[j] = true; // 标记 j 为已被加入过队列
	q.push(j); // 将 v 入队
	}
	}
	}
	}

	void BFSTrave() // 遍历图 G
	{
	for(int u = 0; u < n; u++) // 枚举所有顶点
	{
	if(inq[u] == false) // 如果 u 未曾加入过队列
	BFS(u); // 遍历 u 所在的连通块
	}
	}

# 邻接表

	vector<int> Adj[MAXV]; // 图 G，Adj [u] 存放从顶点 u 出发可以到达的所有顶点
	int n; //n 为顶点数，MAXV 为最大顶点数
	bool inq[MAXV] = {false}; // 若顶点 i 曾入过队列，则 inq [i]==true。初值为 false

	void BFS(int u)
	{
	queue<int> q;
	q.push(u);
	inq[u] = true;

	while(!q.empty())
	{
	int v = q.front();
	q.pop();

	for(int j = 0; j < Adj[v].size(); j++)
	{
	int i = Adj[v][j];
	if(!inq[i])
	{
	q.push(i);
	inq[i] = true;
	}
	}
	}
	}

	void BFSTrave()
	{
	for(int u = 0; u < n; u++)
	{
	if(inq[u] == false)
	BFS(u);
	}
	}

DFS 传入的是未访问的顶点，在 DFS 函数中进行访问；BFS 传入的是未访问的顶点，入队的是访问过的顶点

# cin 放在 while 条件中

	#include <iostream>
	using namespace std;
	int main(void)
	{
	char ch;

	while (cin >> ch)
	{
	cout << ch << endl;
	}
	}

当读到 ctrl + Z 时退出循环

# 二叉排序树

	struct node{
	typename data; // 数据域
	node * lchild; // 指向左子树根结点的指针
	node * rchild; // 指向右子树根结点的指针
	};

	node * newNode(int v)
	{
	node * Node = new node; // 申请一个 node 型变量的地址空间
	Node->data = v; // 结点权值为 v
	Node->lchild = Node->rchild = NULL; // 初始状态下没有左右孩子
	return Node; // 返回新建结点的地址
	}

# 查找

	//search 函数查找二叉查找树中数据域为 x 的结点
	void search(node * root, int x)
	{
	if(root == NULL) // 空树，查找失败
	{
	printf("search failed");
	return;
	}
	else
	{
	if(x == root->data) // 查找成功，访问之
	{
	printf("%d", root->data);
	}
	else if(x < root->data) // 如果 x 比根结点的数据域小，说明 x 在左子树
	search(root->lchild, x); // 往左子树搜索 x
	else if(x > root->data) // 如果 x 比根结点的数据域大，说明 x 在右子树
	search(root->rchild, x); // 往右子树搜索 x
	}
	}

# 插入

	//insert 函数将在二叉树中插入一个数据域为 x 的新结点（注意参数 root 要加引用 & amp;）
	void insert(node* &root, int x)
	{
	if(root == NULL) // 空树，说明查找失败，也即插入位置
	{
	root = newNode(x); // 新建结点
	return;
	}
	else
	{
	if(root->data == x) // 查找成功，说明结点已存在，直接返回
	return;
	else if(x < root->data) // 如果 x 比根结点的数据域小，说明 x 需要插在左子树
	insert(root->lchild, x); // 往左子树搜索 x
	else if(x > root->data) // 如果 x 比根结点的数据域大，说明 x 需要插在右子树
	insert(root->rchild, x); // 往右子树搜索 x
	}


	}

# 建立

	node* Create(int data[], int n)
	{
	node* root = NULL; // 新建根结点 root
	for(int i = 0; i < n; i++)
	insert(root, data[i]);

	return root; // 返回根结点
	}

注意，即便是一组相同的数字，如果插入它们的顺序不同，最后生成的二叉查找树也可能不同。

# 删除

把以二叉查找树中比结点权值小的最大节点称为该结点的前驱（该结点左子树中的最右节点），而把比结点权值大的最小结点称为该结点的后继（右子树的最左结点）。

	// 寻找以 root 为根结点的树中的最大权值结点
	node* findMax(node* root)
	{
	while(root->rchild != NULL)
	root = root->rchild; // 不断往右，直到没有右孩子

	return root;
	}

	// 寻找以 root 为根结点的树中的最小权值结点
	node* findMin(node* root)
	{
	while(root->lchild != NULL)
	root = root->lchild; // 不断往左，直到没有左孩子
	return root;
	}

	// 删除以 root 为根结点的树中权值为 x 的结点
	void deleteNode(node* &root, int x)
	{
	if(root == NULL) // 不存在权值为 x 的结点
	return;
	else
	{
	if(root->data == x) // 找到欲删除结点
	{
	if(root->lchild == NULL && root->rchild == NULL) // 叶子结点，直接删除
	{
	root = NULL; // 把 root 地址设为 NULL，父结点就引用不到它了
	}
	else if(root->lchild != NULL) // 左子树不为空
	{
	node* pre = findMax(root->lchild); // 找 root 前驱
	root->data = pre->data; // 用前驱覆盖 root
	deleteNode(root->lchild, pre->data); // 在左子树中删除结点 pre
	}
	else // 右子树不为空
	{
	node* next = findMin(root->rchild); // 找 root 后继
	root->data = next->data; // 用后继覆盖 root
	deleteNode(root->rchild, next->data); // 在右子树中删除结点 next
	}
	}
	else if(x < root->data)
	deleteNode(root->lchild, x); // 在左子树中删除 x
	else
	deleteNode(root->rchild, x); // 在右子树中删除 x
	}
	}

# 平衡二叉树

存储

	struct node{
	int v, height; //v 为结点权值，height 为当前子树高度
	node* rchild, lchild; // 左右孩子结点的地址
	};

新建一个结点

	// 生成一个新结点，v 为结点权值
	node* newNode(int v)
	{
	node* Node = new node; // 申请一个 node 型变量的地址空间
	Node->v = v; // 结点权值为 v
	Node->height = 1; // 结点高度初始为 1
	Node->rchild = Node->lchild = NULL; // 初始状态下没有左右孩子
	return Node; // 返回新建结点的地址
	}

	// 获取以 root 为根结点的子树的当前 height
	int getHeight(node* root)
	{
	if(root == NULL)
	return 0; // 空结点高度为 0
	return root->height;
	}

	// 计算结点 root 的平衡因子
	int getBalanceFactor(node* root)
	{
	// 左子树高度减右子树高度
	return getHeight(root->lchild) - getHeight(root->rchild);
	}

	// 更新结点 root 的 height
	void updateHeight(node* root)
	{
	//max (左孩子的 height, 右孩子的 height) + 1
	root->height = max(getHeight(root->lchild), getHeight(root->rchild)) + 1;
	}

# 查找

	//search 函数查找 AVL 树中数据域为 x 的结点
	void search(node * root, int x)
	{
	if(root == NULL) // 空树，查找失败
	{
	printf("search failed");
	return;
	}
	else
	{
	if(x == root->data) // 查找成功，访问之
	{
	printf("%d", root->data);
	}
	else if(x < root->data) // 如果 x 比根结点的数据域小，说明 x 在左子树
	search(root->lchild, x); // 往左子树搜索 x
	else if(x > root->data) // 如果 x 比根结点的数据域大，说明 x 在右子树
	search(root->rchild, x); // 往右子树搜索 x
	}
	}

# 插入

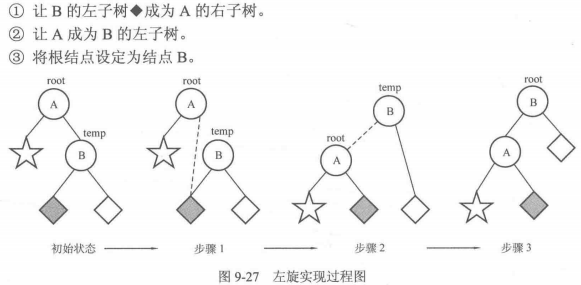
	// 左旋（Left Rotation）
	void L(node* &root)
	{
	node* temp = root->rchild; //root 指向结点 A，temp 指向结点 B
	root->rchild = temp->lchild; // 步骤 1
	temp->lchild = root; // 步骤 2
	updateHeight(root); // 更新结点 A 的高度
	updateHeight(temp); // 更新结点 B 的高度
	root = temp; // 步骤 3
	}

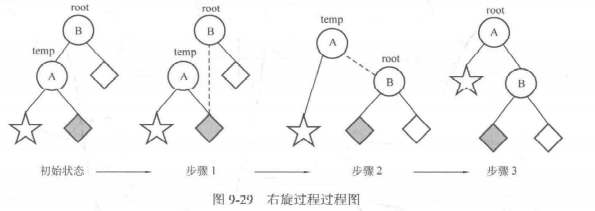
	// 右旋（Right Rotation）
	void R(node* root)
	{
	node* temp = root->lchild; //root 指向结点 B，temp 指向结点 A
	root->lchild = temp->rchild; // 步骤 1
	temp->rchild = root; // 步骤 2
	updateHeight(root); // 更新结点 B 的高度
	updateHeight(temp); // 更新结点 A 的高度
	root = temp; // 步骤 3
	}

左右旋都是上位操作

只要把最靠近插入结点的失衡结点调整到正常，路径上的所有结点就都会平衡。

树型	判定条件	调整方法
LL	BF(root)= 2, BF(root->lchild)=1	对 root 进行右旋
LR	BF(root) = 2, BF(root->lchild) = -1	先对 root->lchild 进行左旋，再对 root 进行右旋
RR	BF(root) = -2, BF(root->rchild) = -1	对 root 进行左旋
RL	BF(root) = -2, BF(root->lchild) = 1	先对 root->rchild 进行右旋，再对 root 进行左旋

由于需要从插入的结点开始从下往上判断结点是否失衡，因此需要在每个 insert 函数之后更新当前子树的高度，并在这之后根据树型来进行平衡操作。

	// 插入权值为 v 的结点
	void insert(node* &root, int v)
	{
	if(root == NULL) // 到达空结点
	{
	root = newNode(v);
	return;
	}
	else
	{
	if(v < root->v) //v 比根结点的权值小
	{
	insert(root->lchild, v); // 往左子树插入
	updateHeight(root); // 更新树高
	if(getBalanceFactor(root) == 2)
	{
	if(getBalanceFactor(root->lchild) == 1) //LL 型
	R(root);
	else if(getBalanceFactor(root->lchild) == -1) //LR 型
	{
	L(root->lchild);
	R(root);
	}
	}
	}
	else if(v > root->v) //v 比根结点的权值大
	{
	insert(v->rchild, v); // 往右子树插入
	updateHeight(root); // 更新树高
	if(getBalanceFactor(root) == -2)
	{
	if(getBalanceFactor(root->rchild) == -1) //RR 型
	L(root);
	else if(getBalanceFactor(root->rchild) == 1) //RL 型
	{
	R(root->rchild);
	L(root);
	}
	}
	}
	}
	}

# 建立

	// 建立
	node* Create(int data[], int n)
	{
	node* root = NULL;
	for(int i = 0; i < n; i++)
	insert(root, data[i]);

	return root;
	}

# 拓扑排序

	vector<int> Adj[MAXV]; // 邻接表
	int n, m, inDegree[MAXV]; // 顶点数，入度

	// 拓扑排序
	bool topologicalSort()
	{
	int num = 0; // 记录加入拓扑排序的顶点数
	queue<int> q;

	for(int i = 0; i < n; i++)
	{
	if(inDegree[i] == 0)
	q.push(i); // 将所有入度为 0 的顶点入队
	}

	while(!q.empty())
	{
	int u = q.front(); // 取队首顶点 u
	q.pop();
	//printf ("% d", u); // 此处可输出顶点 u，作为拓扑序列中的顶点
	for(int i = 0; i < Adj[u].size(); i++)
	{
	int v = Adj[u][i]; //u 的后继顶点 v
	inDegree[v]--; // 顶点 v 的入度减 1
	if(inDegree[v] == 0) // 顶点 v 的入度减为 0 则入队
	q.push(v);
	}
	Adj[u].clear(); // 清空顶点 u 的所有出边（如无必要可不写）
	num++; // 加入拓扑序列的顶点数加 1
	}

	if(num == n)
	return true; // 加入拓扑序列的顶点数为 n，说明拓扑排序成功
	else
	return false; // 加入拓扑序列的顶点数小于 n，说明拓扑排序失败
	}

应用：判断给定的图是否是有向无环图

如果要求有多个入度为 0 的顶点，选择编号最小的顶点，那么把 queue 改成 priority_queue，并保持队首元素（堆顶元素）是优先队列中最小的元素即可。（用 set 也是可以的）

注意：

# KMP 算法

# next 数组

next[i]表示子串s[0...i]的前缀s[0...k]等于后缀s[i-k...i]的最大的k，前缀跟后缀可以部分重叠，但是不能等于s[0...i]本身。如果找不到相等的前后缀，那么就令next[i] = -1。显然，next[i]就是所求最长相等前后缀中前缀最后一位的下标。

next 数组的求解过程

初始化 next 数组，令 j = next [0] = -1.
让 i 在 1 ~ len - 1 范围遍历，对每个 i，执行 3.4.，以求解 next [i]。
不断令 j = next [j]，知道 j 回退为 - 1，或是 s [i] = s [j + 1] 成立。
如果 s [i] = s [j + 1]，则 next [i] = j + 1；否则 next [i] = j。

	//getNext 求解长度为 len 的字符串 s 的 next 数组
	void getNext(char s[], int len)
	{
	int j = -1;
	next[0] = -1; // 初始化 j = next [0] = -1

	for(int i = 1; i < len; i++) // 求解 next [1] ~ next [len - 1]
	{
	while(j != -1 && s[j + 1] != s[i])
	j = next[j]; // 反复令 j = next [j]，直到 j 回退到 - 1，或是 s [i]==s [j+1]

	if(s[j + 1] == s[i])
	j++; // 如果 s [j+1]==s [i]，则 next [i]=j+1，先令 j 指向这个位置
	next[i] = j;
	}
	}

# KMP 算法

思路：

初始化 j = -1，表示 pattern 当前已被匹配的最后位。
让 i 遍历文本串 text，对每个 i，执行 3.4. 来试图匹配 text [i] 和 pattern [j + 1]。
不断令 j = next [j]，知道 j 回退为 - 1，或是 text [i] == pattern [j + 1] 成立。
如果 text [i] == pattern [j + 1]，则令 j++。如果 j 达到 m - 1，说明 pattern 是 text 的子串，返回 true。

	//KMP 算法，判断 pattern 是否是 text 的子串
	bool KMP(char text[], char pattern[])
	{
	int n = strlen(text), m = strlen(pattern); // 字符串长度
	getNext(pattern, m); // 计算 pattern 的 next 数组
	int j = -1; // 初始化 j 为 - 1，表示当前还没有一位被匹配
	for(int i = 0; i < n; i++) // 试图匹配 text [i]
	{
	while(j != -1 && pattern[j + 1] != text[i])
	j = next[j]; // 不断回退，直到 j 回到 - 1 或 text [i] == pattern [j+1]

	if(pattern[j+1] == text[i])
	j++; //text [i] 与 pattern [j+1] 匹配成功，令 j 加 1

	if(j == m - 1) //pattern 完全匹配，说明 pattern 是 text 的子串
	return true;
	}
	return false; // 执行完 text 还没匹配成功，说明 pattern 不是 text 的子串
	}

求解 next 数组的过程其实就是模式串 pattern 进行自我匹配的过程

	//KMP 算法，统计 pattern 在 text 中出现的次数
	int KMP(char text[], char pattern[])
	{
	int n = strlen(text), m = strlen(pattern);
	int j = -1;
	int ans = 0; // 表示成功匹配次数
	getNext(pattern, m);
	for(int i = 0; i < n; i++)
	{
	while(j != -1 && pattern[j+1] != text[i])
	j = next[j];

	if(pattern[j+1] == text[i])
	j++;

	if(j == m-1) //pattern 完全匹配，说明 pattern 是 text 的子串
	{
	ans++; // 成功匹配次数加 1
	j = next[j]; // 让 j 回退到 next [j] 继续匹配
	}
	}
	return ans; // 返回成功匹配
	}

# 分块思想

算法基础

# 差分序列

# 前言

# 原理

# 代码示例

# RMQ

# 问题描述

# 算法描述

# 初始化

# 查询

# 单调栈

# 归并排序

# 快速排序

# 随机数

# 并查集

# 初始化

# 查找

# 合并

# 路径压缩

# 种类并查集

# 最小生成树

# prim 算法

# 链式前向星

# 单调队列

# 进制哈希

# 最短路径

# Dijkstra 算法

# 新增边权

# 新增点权

# 最短路径条数

# Dijkstra + DFS

# DFS

# BF 算法

# spfa

# Floyd 算法

# DFS 和 BFS

# DFS

# BFS

# 邻接表

# cin 放在 while 条件中

# 二叉排序树

# 查找

# 插入

# 建立

# 删除

# 平衡二叉树

# 查找

# 插入

# 建立

# 拓扑排序

# KMP 算法

# next 数组

# KMP 算法

# 分块思想

bert

算法2