首页

# 剑指 Offer 28. 对称的二叉树

1692707384014

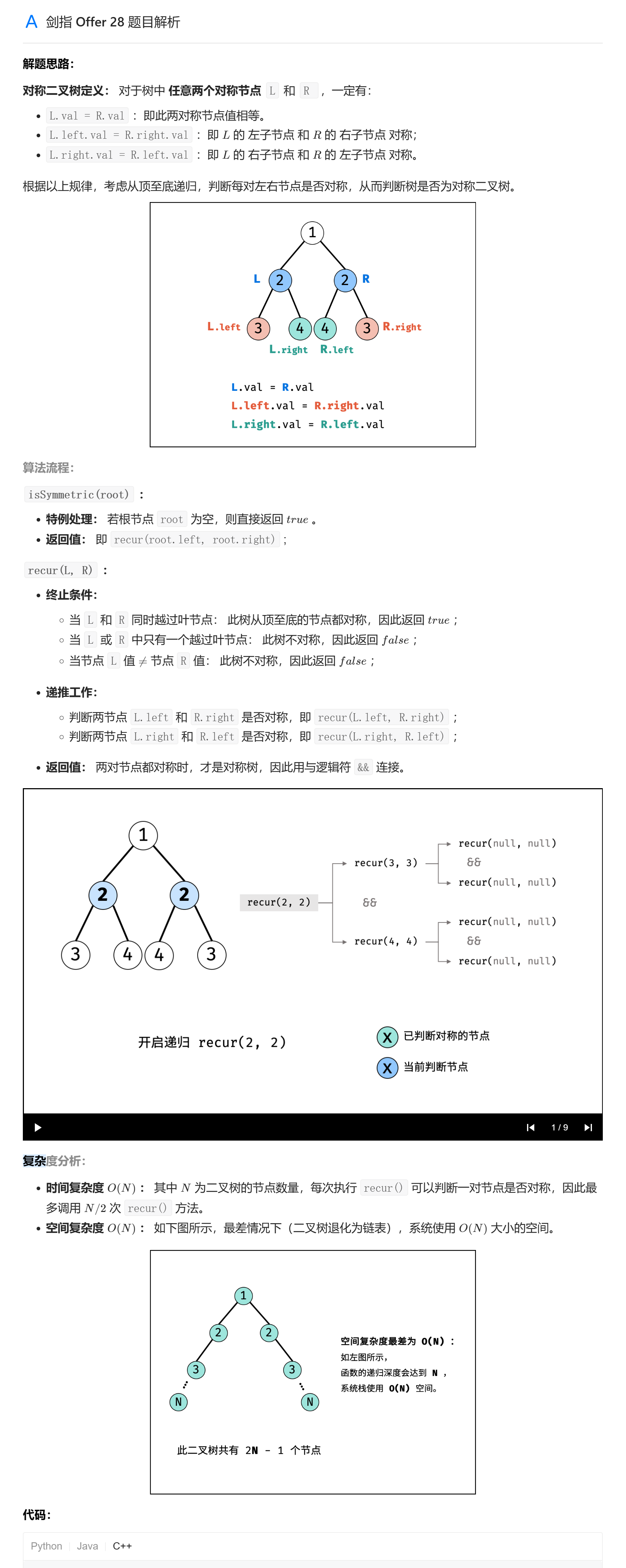
1692707742822

越过叶节点就是传入的指针为空。

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        return root == nullptr || recur(root->left, root->right);
    }
private:
    bool recur(TreeNode* L, TreeNode* R) {
        if(L == nullptr && R == nullptr) return true;
        if(L == nullptr || R == nullptr || L->val != R->val) return false;
        return recur(L->left, R->right) && recur(L->right, R->left);
    }
};

# 剑指 Offer 32 - I. 从上到下打印二叉树

1692709248141

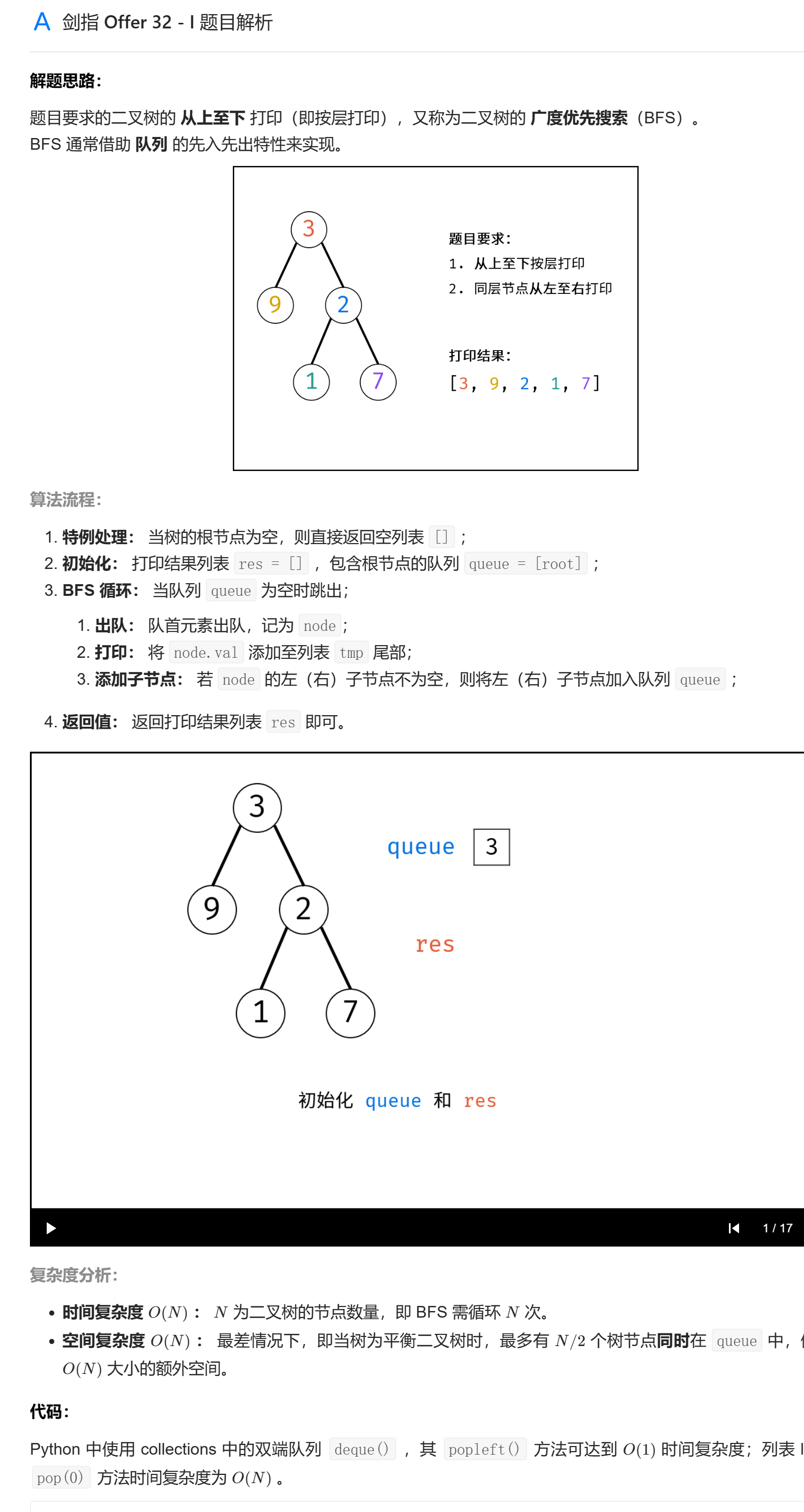
1692709269363

class Solution {
public:
    vector<int> levelOrder(TreeNode* root) {
        vector<int> res;
        if(!root) return res;
        queue<TreeNode*> que;
        que.push(root);
        while(!que.empty()){
            TreeNode* node = que.front();
            que.pop();
            res.push_back(node->val);
            if(node->left) que.push(node->left);
            if(node->right) que.push(node->right);
        }
        return res;
    }
};

# 剑指 Offer 32 - II. 从上到下打印二叉树 II

1692711272545

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
// class Solution {
// public:
//     vector<vector<int>> levelOrder(TreeNode* root) {
//     }
// };
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int> > res;
        if (root == NULL)
            return res;
        queue<TreeNode*> q;
        q.push(root);
        q.push(NULL);
        vector<int> temp;
        TreeNode* temp_ptr;
        while (!q.empty()) {
            temp_ptr = q.front();
            q.pop();
            
            if (temp_ptr == NULL) {
                // 遍历一行结束
                res.push_back(temp);
                temp.clear();
                if (q.size()) {
                    q.push(NULL);
                }
                // 如果队列中已经没有结点指针了，说明遍历完了，不用再加 NULL 标志
            }
            else {
                temp.push_back(temp_ptr->val);
                if (temp_ptr->left)
                    q.push(temp_ptr->left);
                if (temp_ptr->right)
                    q.push(temp_ptr->right);
            }
        }
        return res;
    }
};
上面算法的思路是在队列中，每一层结点之后加一个 NULL 作为标记。
vector 的 push_back 是深拷贝的，所有 temp 清空后，已经 push_back 进入队列的列表不变。
1692712429574
1692712438812
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> que;
        vector<vector<int>> res;
        int cnt = 0;
        if(root != NULL) que.push(root);
        while(!que.empty()) {
            vector<int> tmp;
            // 注意这里，利用减减，先初始化 i，因为 que 的长度会发生变化
            for(int i = que.size(); i > 0; --i) {
                root = que.front();
                que.pop();
                tmp.push_back(root->val);
                if(root->left != NULL) que.push(root->left);
                if(root->right != NULL) que.push(root->right);
            }
            res.push_back(tmp);
        }
        return res;
    }
};
# 剑指 Offer 32 - III. 从上到下打印二叉树 III
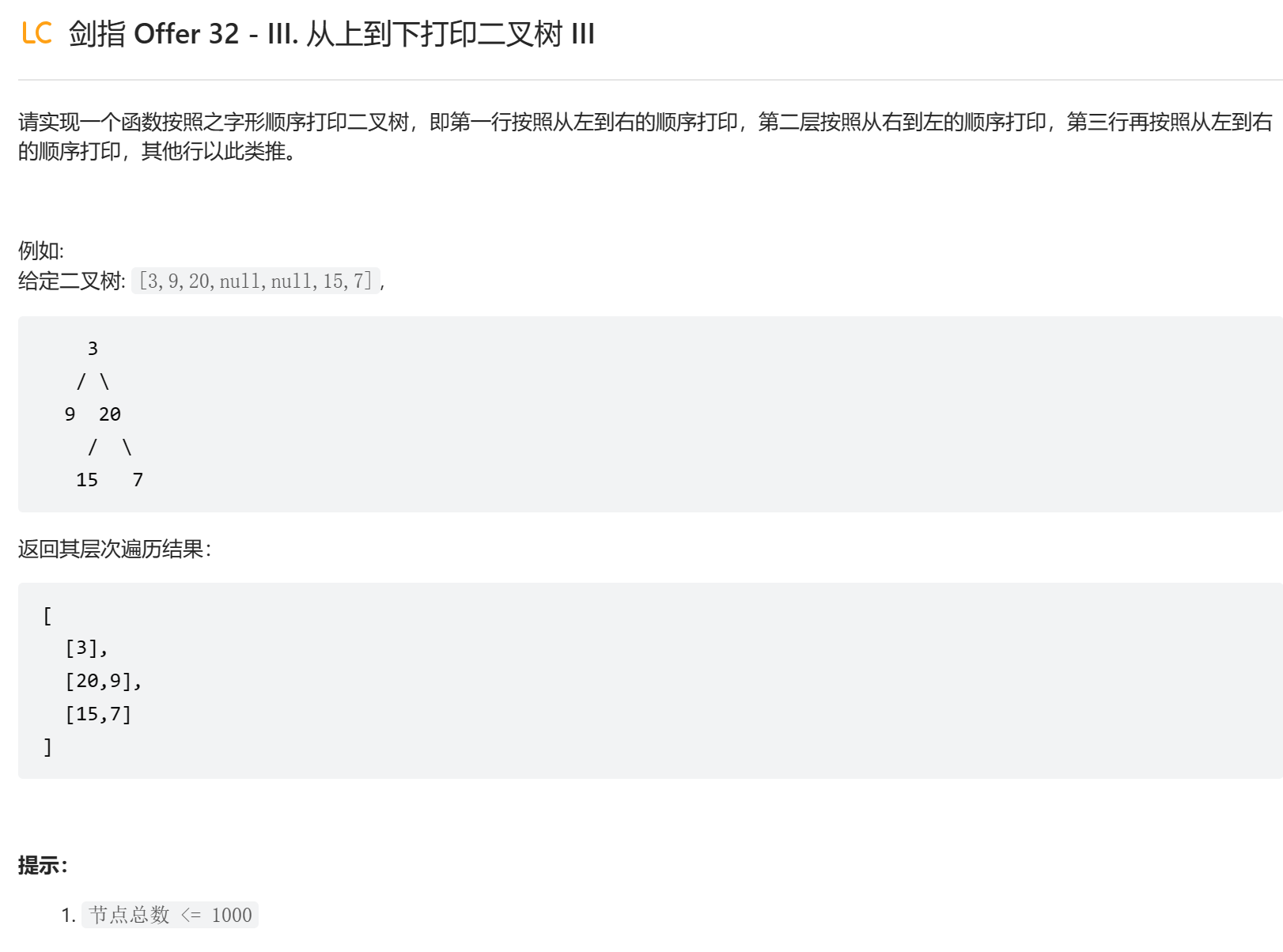
1692716725551
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
// class Solution {
// public:
//     vector<vector<int>> levelOrder(TreeNode* root) {
//     }
// };
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int> > res;
        queue<TreeNode*> q;
        if (root != NULL)
            q.push(root);
        int flag = 1;
        while (!q.empty()) {
            TreeNode* p = NULL;
            
            vector<int> temp;
            for (int i = q.size(); i > 0; i--) {
                p = q.front();
                q.pop();
                temp.push_back(p->val);
                if (p->left)
                    q.push(p->left);
                if (p->right)
                    q.push(p->right);
            }
            if (flag) {
                res.push_back(temp);
                flag = 0;
            }
            else {
                reverse(temp.begin(), temp.end());
                res.push_back(temp);
                flag = 1;
            }
        }  
        return res;
    }
};
上面的算法是新添加了一个标记和一个 reverse 函数（用来反转 vector），但返回 vector res 的 size 本身就是一个标记，可以直接用，如下面的解析：
1692718220134
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        deque<TreeNode*> deque;
        vector<vector<int>> res;
        if(root != NULL) deque.push_back(root);
        while(!deque.empty()) {
            // 打印奇数层
            vector<int> tmp;
            for(int i = deque.size(); i > 0; i--) {
                // 从左向右打印
                TreeNode* node = deque.front();
                deque.pop_front();
                tmp.push_back(node->val);
                // 先左后右加入下层节点
                if(node->left != NULL) deque.push_back(node->left);
                if(node->right != NULL) deque.push_back(node->right);
            }
            res.push_back(tmp);
            if(deque.empty()) break; // 若为空则提前跳出
            // 打印偶数层
            tmp.clear();
            for(int i = deque.size(); i > 0; i--) {
                // 从右向左打印
                TreeNode* node = deque.back();
                deque.pop_back();
                tmp.push_back(node->val);
                // 先右后左加入下层节点
                if(node->right != NULL) deque.push_front(node->right);
                if(node->left != NULL) deque.push_front(node->left);
            }
            res.push_back(tmp);
        }
        return res;
    }
};
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> que;
        vector<vector<int>> res;
        if(root != NULL) que.push(root);
        while(!que.empty()) {
            vector<int> tmp;
            for(int i = que.size(); i > 0; i--) {
                TreeNode* node = que.front();
                que.pop();
                tmp.push_back(node->val);
                if(node->left != NULL) que.push(node->left);
                if(node->right != NULL) que.push(node->right);
            }
            if(res.size() % 2 == 1) reverse(tmp.begin(),tmp.end());
            res.push_back(tmp);
        }
        return res;
    }
};
# 剑指 Offer 55 - I. 二叉树的深度
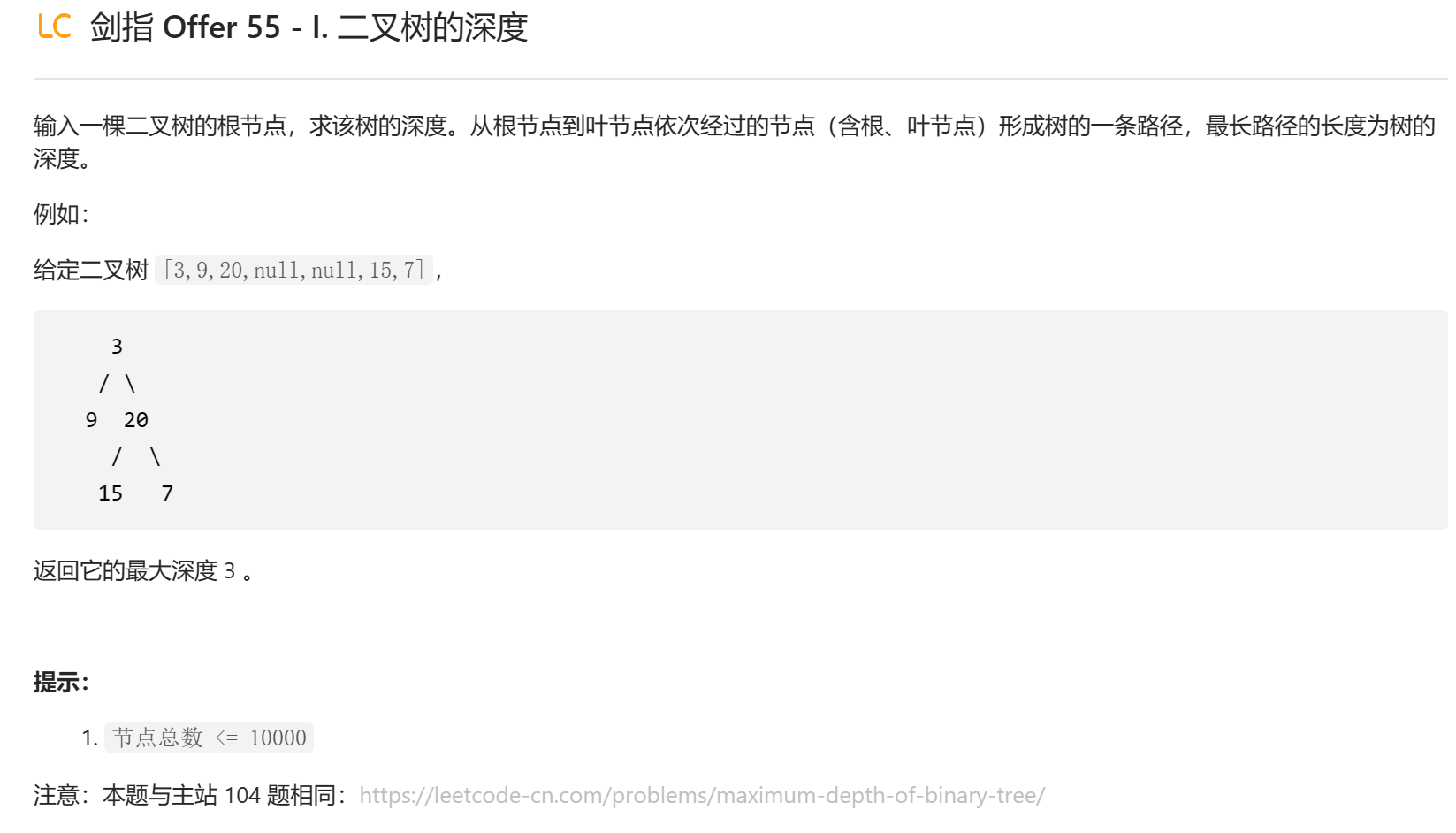
1692719466029
1692719502269
1692719510682
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root == nullptr) return 0;
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;
    }
};
1692719883631
1692719892338
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root == nullptr) return 0;
        vector<TreeNode*> que;
        que.push_back(root);
        int res = 0;
        while(!que.empty()) {
            vector<TreeNode*> tmp;
            for(TreeNode* node : que) {
                if(node->left != nullptr) tmp.push_back(node->left);
                if(node->right != nullptr) tmp.push_back(node->right);
            }
            que = tmp;
            res++;
        }
        return res;
    }
};
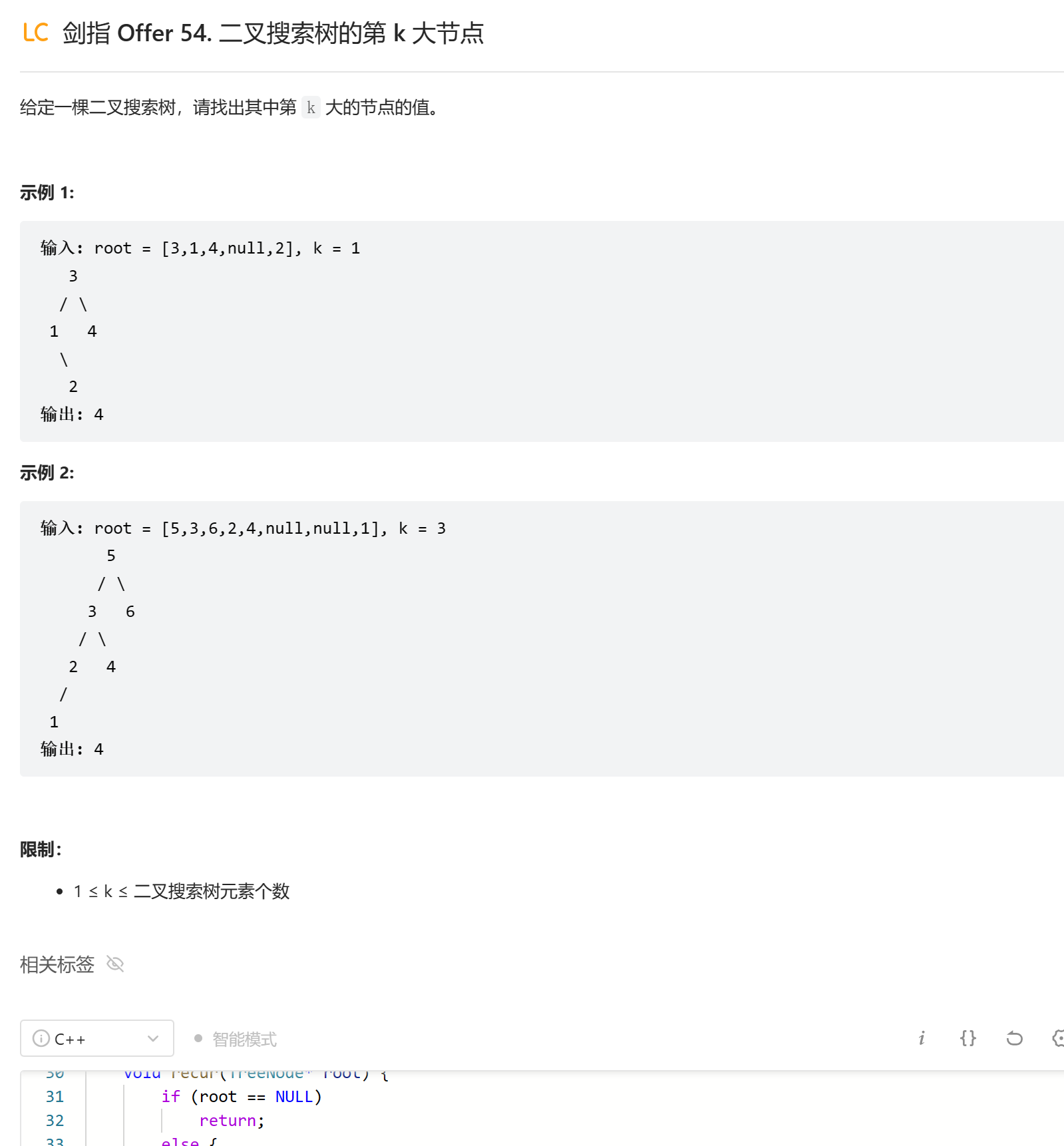
# 剑指 Offer 54. 二叉搜索树的第 k 大节点
1692721950163
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
// class Solution {
// public:
//     int kthLargest(TreeNode* root, int k) {
//     }
// };
class Solution {
public:
    int kthLargest(TreeNode* root, int k) {
        recur(root);
        if (ve.size() < k) {
            return 0;
        }
        else {
            return ve[k - 1];
        }
    }
private:
    vector<int> ve;
    void recur(TreeNode* root) {
        if (root == NULL)
            return;
        else {
            recur(root->right);
            ve.push_back(root->val);
            recur(root->left);
        }
    }
};
上面的代码没有使用剪枝
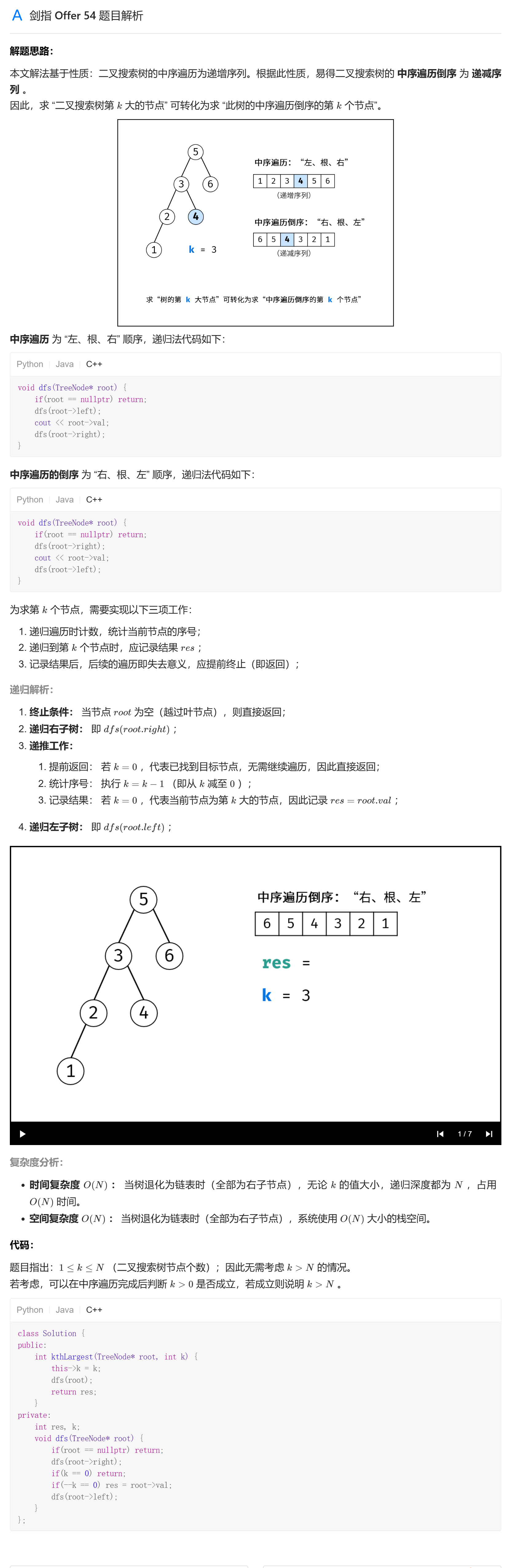
1692722257324
class Solution {
public:
    int kthLargest(TreeNode* root, int k) {
        this->k = k;
        dfs(root);
        return res;
    }
private:
    int res, k;
    void dfs(TreeNode* root) {
        if(root == nullptr) return;
        dfs(root->right);
        if(k == 0) return;
        if(--k == 0) res = root->val;
        dfs(root->left);
    }
};
# 剑指 Offer 55 - II. 平衡二叉树
1692723321673
1692723866623
1692723876833
class Solution {
public:
    bool isBalanced(TreeNode* root) {
        return recur(root) != -1;
    }
private:
    int recur(TreeNode* root) {
        if (root == nullptr) return 0;
        int left = recur(root->left);
        if(left == -1) return -1;
        int right = recur(root->right);
        if(right == -1) return -1;
        return abs(left - right) < 2 ? max(left, right) + 1 : -1;
    }
};
1692723905175
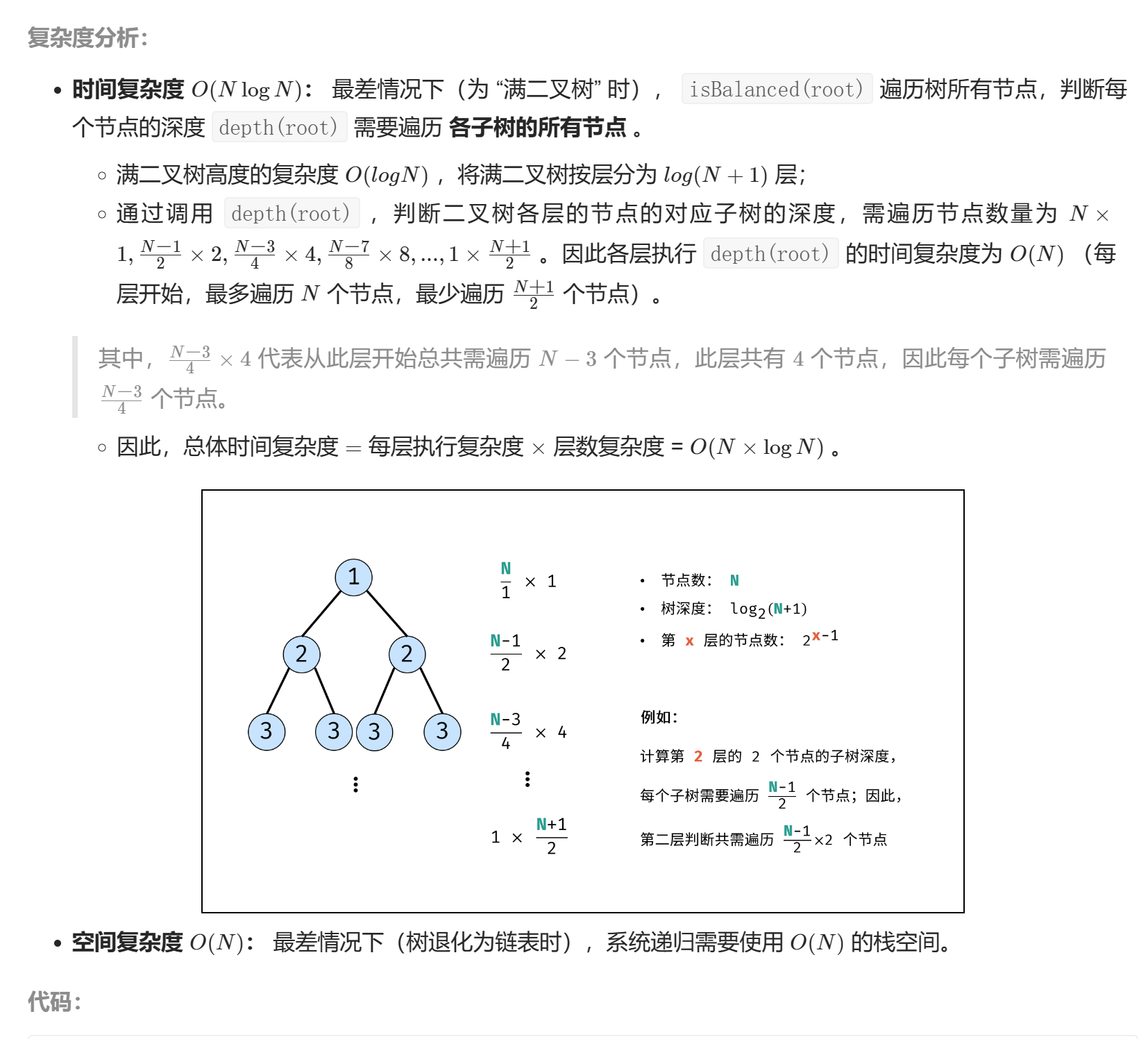
1692723918958
class Solution {
public:
    bool isBalanced(TreeNode* root) {
        if (root == nullptr) return true;
        return abs(depth(root->left) - depth(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right);
    }
private:
    int depth(TreeNode* root) {
        if (root == nullptr) return 0;
        return max(depth(root->left), depth(root->right)) + 1;
    }
};
# 剑指 Offer 68 - I. 二叉搜索树的最近公共祖先