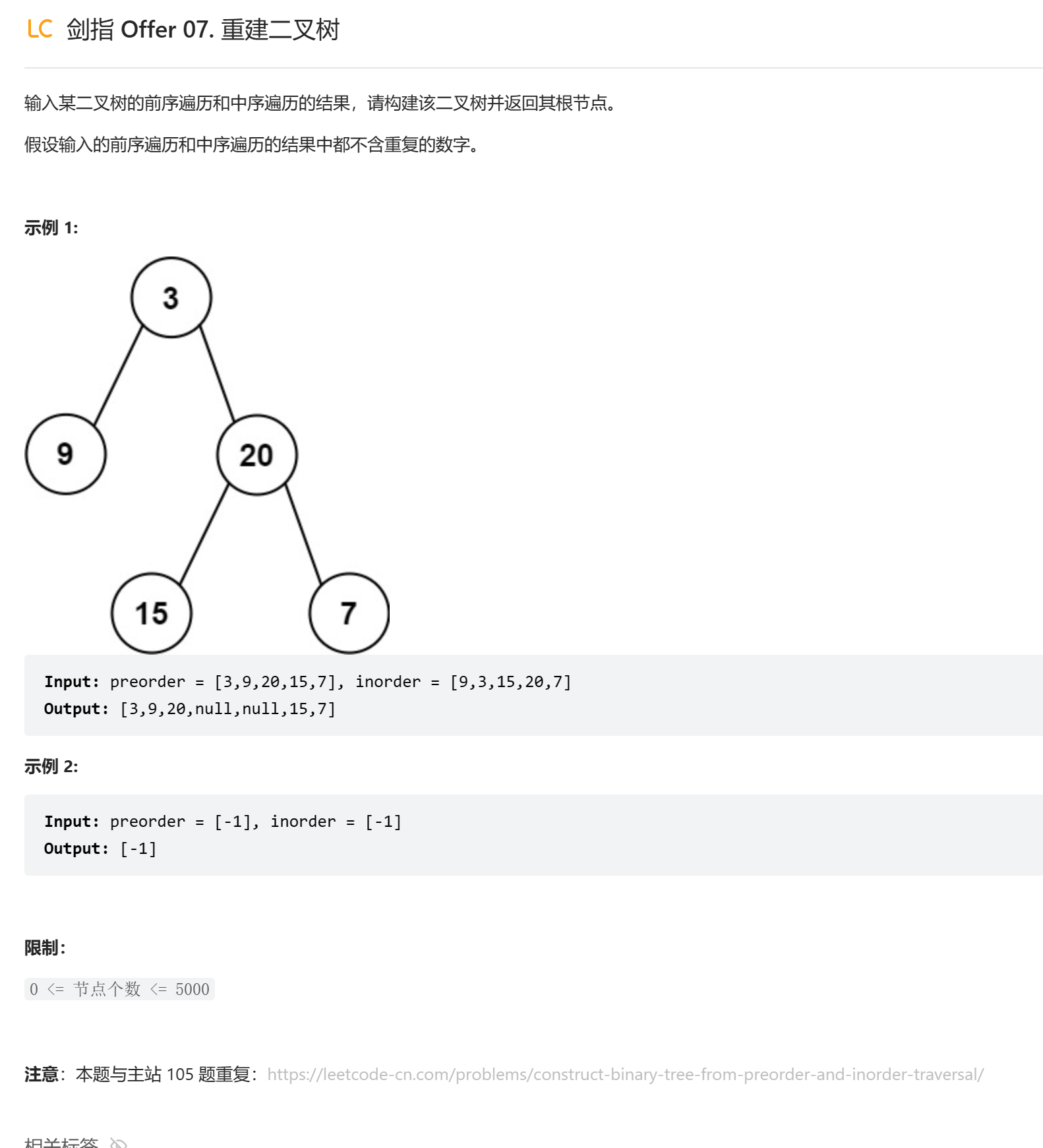
# 剑指 Offer 07. 重建二叉树
dic 是树的结点值对在中序遍历的索引的映射
class Solution { | |
public: | |
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) { | |
this->preorder = preorder; | |
this->inorder = inorder; | |
for (int i = 0; i < inorder.size(); i++) { | |
this->mp[inorder[i]] = i; | |
} | |
return build(0, preorder.size() - 1, 0, inorder.size() - 1); | |
} | |
private: | |
vector<int> preorder; | |
vector<int> inorder; | |
map<int, int> mp; // 结点值到中序遍历中索引的映射 | |
TreeNode* build(int pl, int pr, int il, int ir) { | |
// 参数是在前序遍历和中序遍历中的闭区间的左端点和右端点 | |
if (pl > pr) | |
return NULL; | |
int root_val = preorder[pl]; | |
int root_index = this->mp[root_val]; | |
TreeNode* root = new TreeNode(root_val); | |
int left_tree_length = root_index - il; | |
int right_tree_length = ir - root_index; | |
root->left = build(pl + 1, pl + left_tree_length, il, root_index - 1); | |
root->right = build(pl + left_tree_length + 1, pr, root_index + 1, ir); | |
return root; | |
} | |
}; |
# 剑指 Offer 51. 数组中的逆序对

class Solution { | |
public: | |
int reversePairs(vector<int>& nums) { | |
this->ve = nums; | |
mergeSort(0, nums.size() - 1); | |
return this->count; | |
} | |
private: | |
int count = 0; | |
vector<int> ve; | |
void mergeSort(int l, int r) { | |
if (l >= r) | |
return; | |
int m = (l + r) / 2; | |
mergeSort(l, m); | |
mergeSort(m + 1, r); | |
vector<int> temp; | |
for (int index = l; index <= r; index++) | |
temp.push_back(this->ve[index]); | |
int i = 0, j = m - l + 1; | |
int length = r - l + 1; | |
for (int index = l; index <= r; index++) { | |
//i 和 j 越界的判断要放在前面,防止循环时出现越界报错 | |
if (i == m - l + 1) { | |
ve[index] = temp[j]; | |
j++; | |
} | |
else if (j == r - l + 1) { | |
ve[index] = temp[i]; | |
i++; | |
} | |
else if (temp[i] > temp[j]) { | |
this->count += r - l - j + 1; | |
ve[index] = temp[i]; | |
i++; | |
} | |
else { | |
ve[index] = temp[j]; | |
j++; | |
} | |
} | |
} | |
}; |
上面的算法是从大到小排序的,下面的解析是从小到大排序的,两者在统计逆序对的数量时不同。

class Solution { | |
public: | |
int reversePairs(vector<int>& nums) { | |
vector<int> tmp(nums.size()); | |
return mergeSort(0, nums.size() - 1, nums, tmp); | |
} | |
private: | |
int mergeSort(int l, int r, vector<int>& nums, vector<int>& tmp) { | |
// 终止条件 | |
if (l >= r) return 0; | |
// 递归划分 | |
int m = (l + r) / 2; | |
int res = mergeSort(l, m, nums, tmp) + mergeSort(m + 1, r, nums, tmp); | |
// 合并阶段 | |
int i = l, j = m + 1; | |
for (int k = l; k <= r; k++) | |
tmp[k] = nums[k]; | |
for (int k = l; k <= r; k++) { | |
if (i == m + 1) | |
nums[k] = tmp[j++]; | |
else if (j == r + 1 || tmp[i] <= tmp[j]) | |
nums[k] = tmp[i++]; | |
else { | |
nums[k] = tmp[j++]; | |
res += m - i + 1; // 统计逆序对 | |
} | |
} | |
return res; | |
} | |
}; |
上面的算法中,开辟了一个和 nums 大小一样的列表 tmp,这样在拷贝的下标操作上会带来方便。
#
class Solution { | |
public: | |
bool verifyPostorder(vector<int>& postorder) { | |
return recur(postorder, 0, postorder.size() - 1); | |
} | |
private: | |
bool recur(vector<int>& postorder, int i, int j) { | |
if(i >= j) return true; | |
int p = i; | |
while(postorder[p] < postorder[j]) p++; | |
int m = p; | |
while(postorder[p] > postorder[j]) p++; | |
return p == j && recur(postorder, i, m - 1) && recur(postorder, m, j - 1); | |
} | |
}; |
当没有右子树或没有左子树的时候,p 将指向根结点。
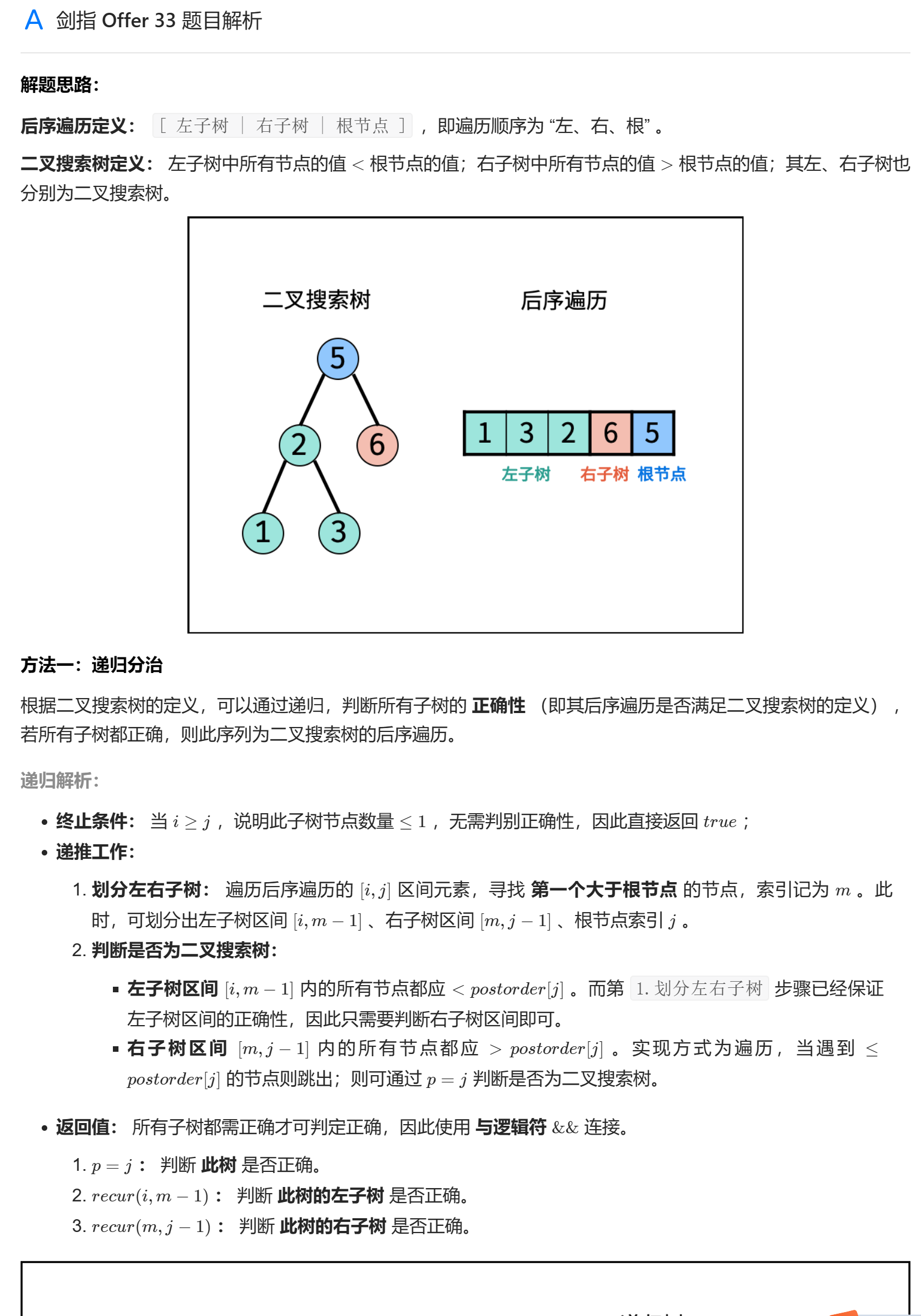
# 剑指 Offer 33. 二叉搜索树的后序遍历序列

class Solution { | |
public: | |
bool verifyPostorder(vector<int>& postorder) { | |
this->postorder = postorder; | |
return recur(0, postorder.size() - 1); | |
} | |
private: | |
vector<int> postorder; | |
bool recur(int l, int r) { | |
// 子树的区间左右端点,闭区间 | |
if (l >= r) | |
return true; | |
int rootVal = this->postorder[r]; | |
int i = l; | |
while (this->postorder[i] <= rootVal && i <= r - 1) { | |
i++; | |
} | |
//i 是第一个大于根结点值的索引 | |
for (int k = i + 1; k <= r - 1; k++) { | |
if (this->postorder[k] < rootVal) | |
return false; | |
} | |
return recur(l, i - 1) && recur(i, r - 1); | |
} | |
}; |
若存在两个结点的值相等的情况,是不影响的。

class Solution { | |
public: | |
bool verifyPostorder(vector<int>& postorder) { | |
return recur(postorder, 0, postorder.size() - 1); | |
} | |
private: | |
bool recur(vector<int>& postorder, int i, int j) { | |
if(i >= j) return true; | |
int p = i; | |
while(postorder[p] < postorder[j]) p++; | |
int m = p; | |
while(postorder[p] > postorder[j]) p++; | |
return p == j && recur(postorder, i, m - 1) && recur(postorder, m, j - 1); | |
} | |
}; |