首页

# 快速排序

1692192746100

1692193001985

1692193017150

1692193032132

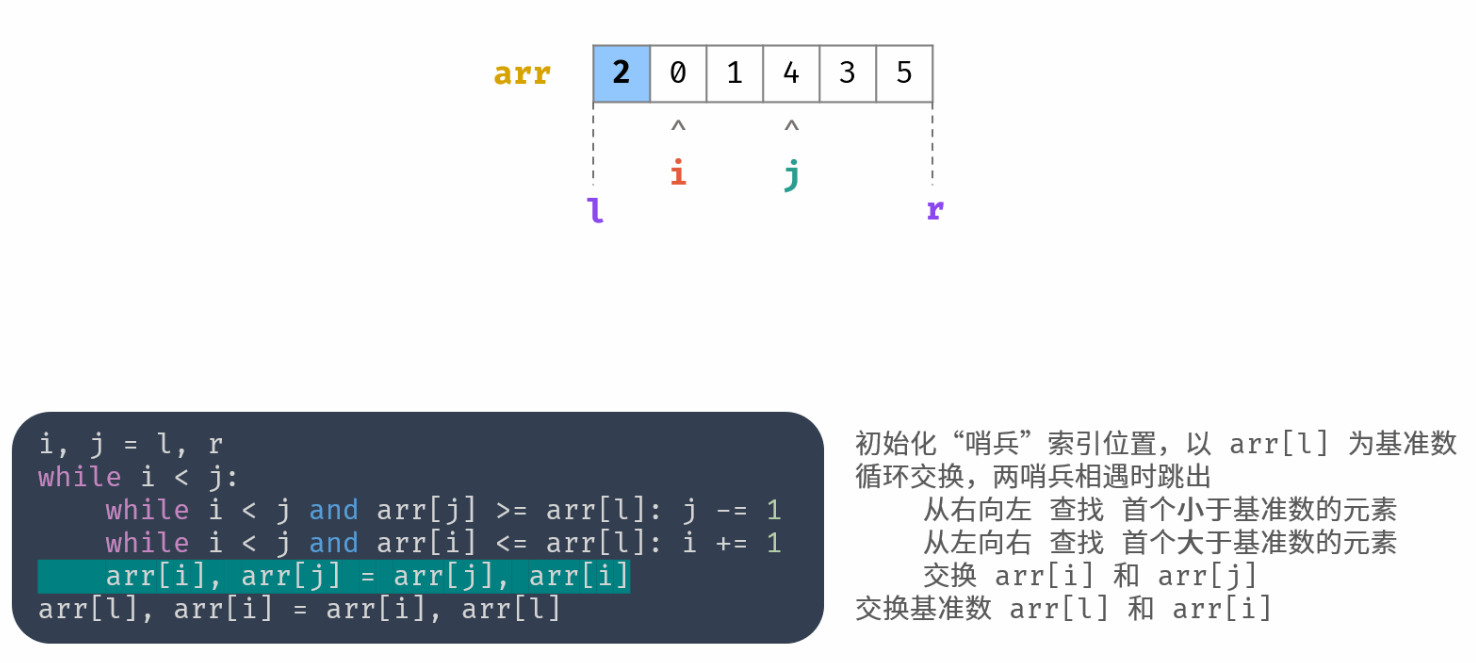
1692193065121

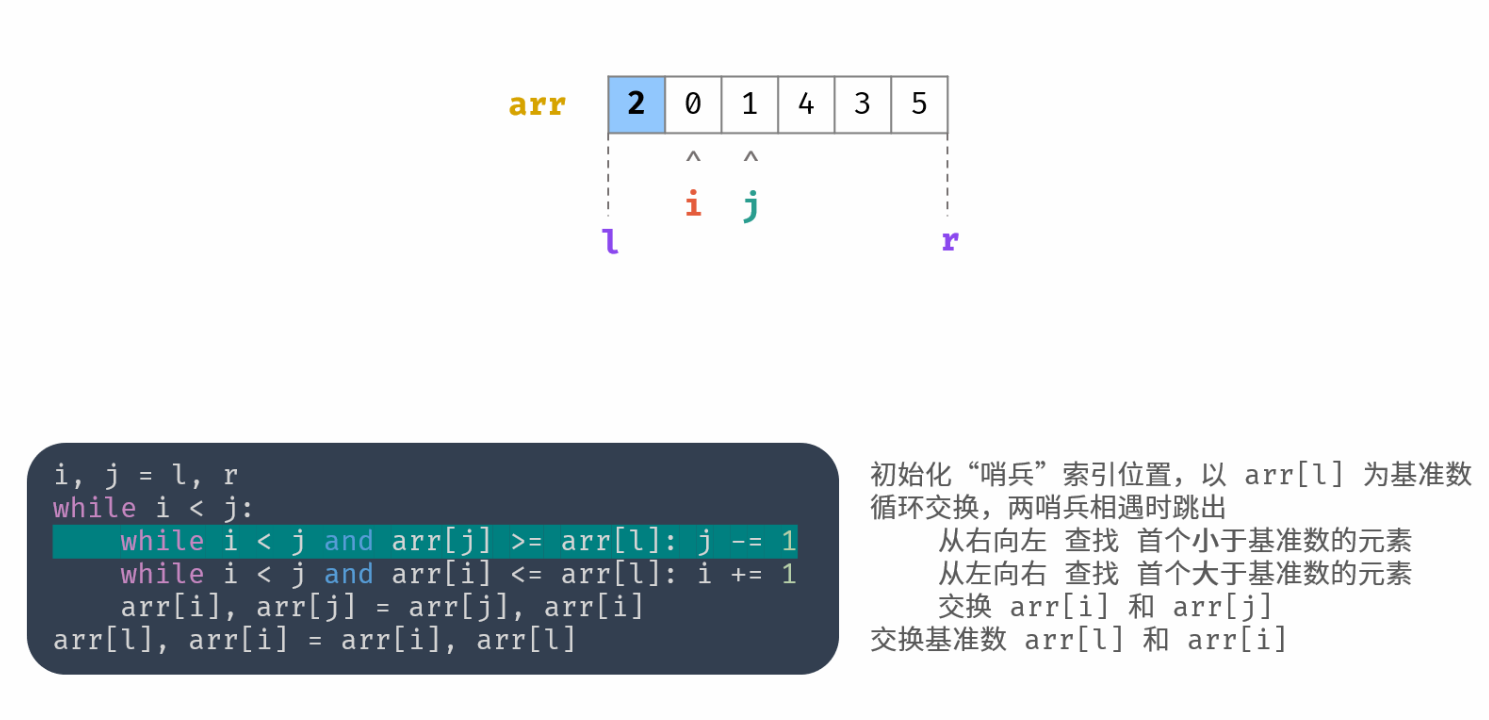
1692193108614

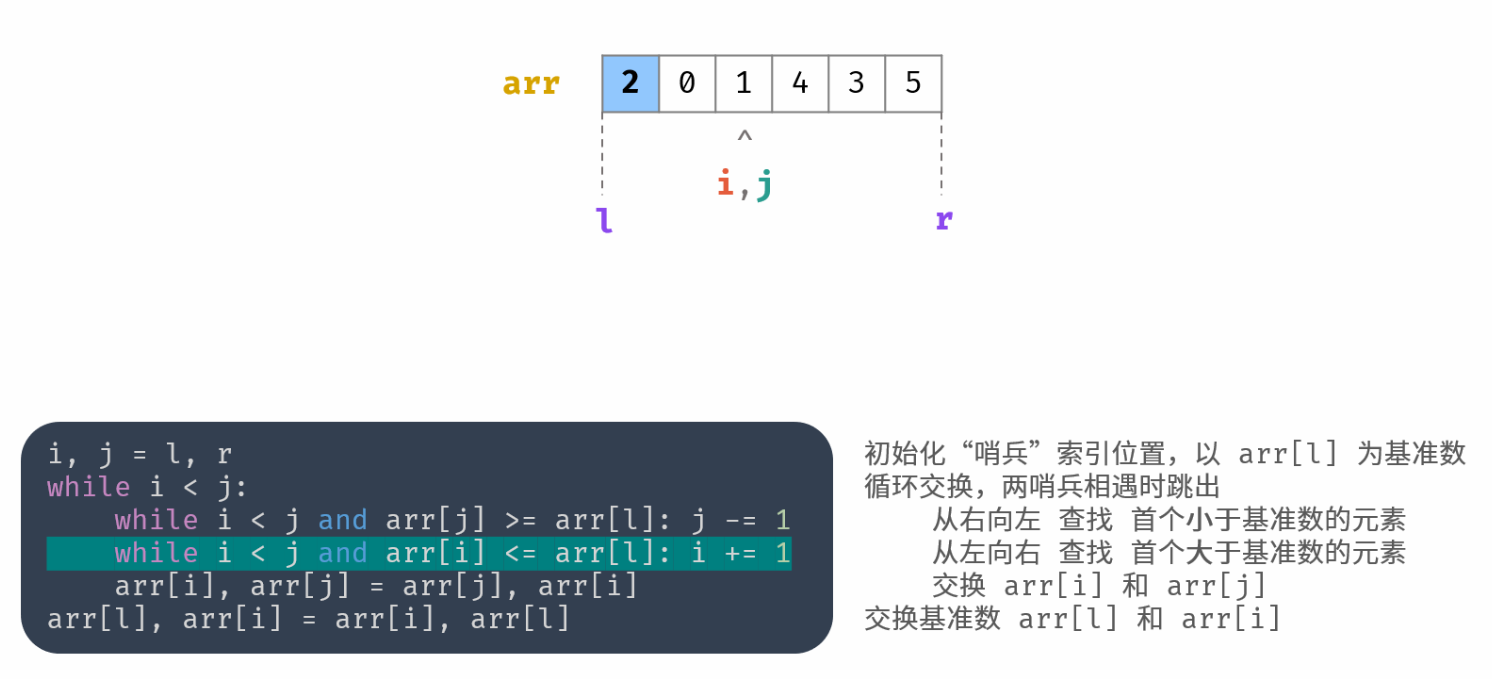
1692193116747

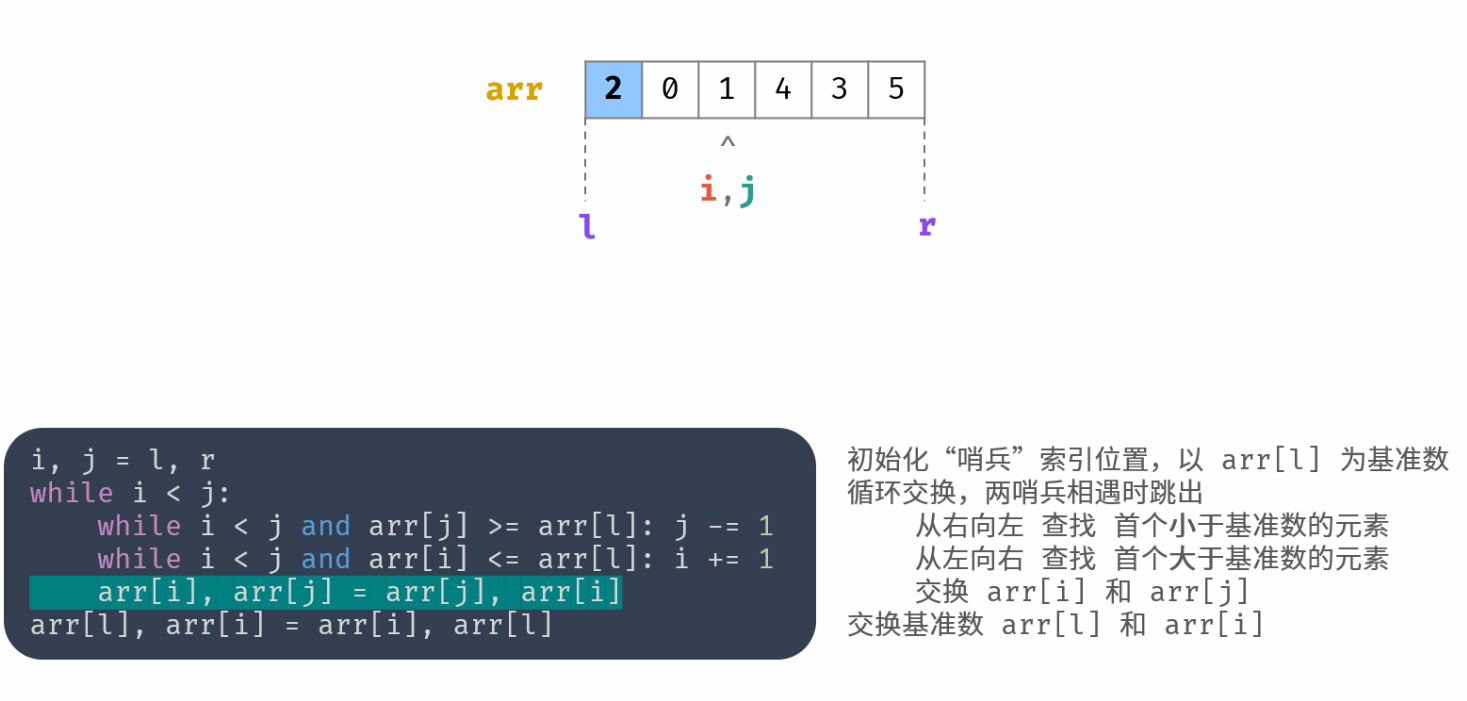
1692193127291

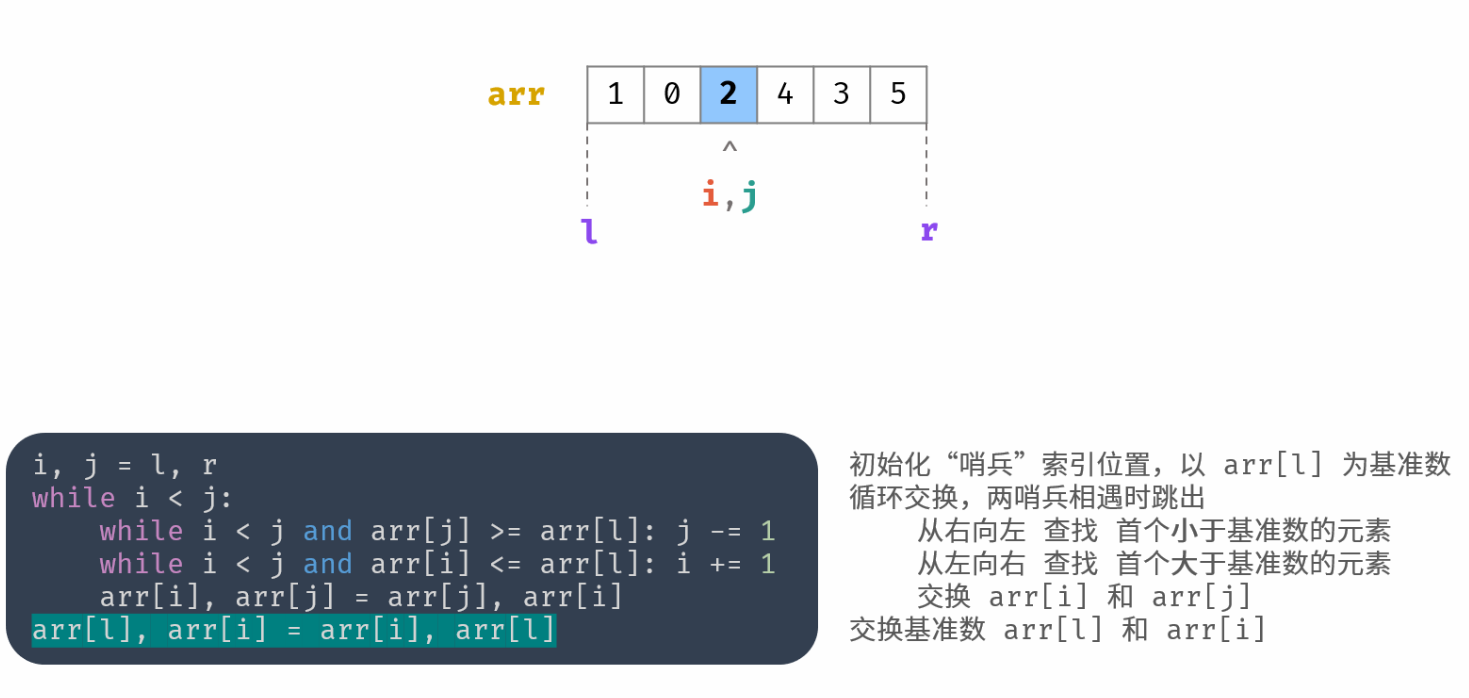
1692193149324

1692193166398

1692193196177

1692193216071

int partition(vector<int>& nums, int l, int r) {
    // 以 nums [l] 作为基准数
    int i = l, j = r;
    while (i < j) {
        while (i < j && nums[j] >= nums[l]) j--;
        while (i < j && nums[i] <= nums[l]) i++;
        swap(nums[i], nums[j]);
    }
    swap(nums[i], nums[l]);
    return i;
}
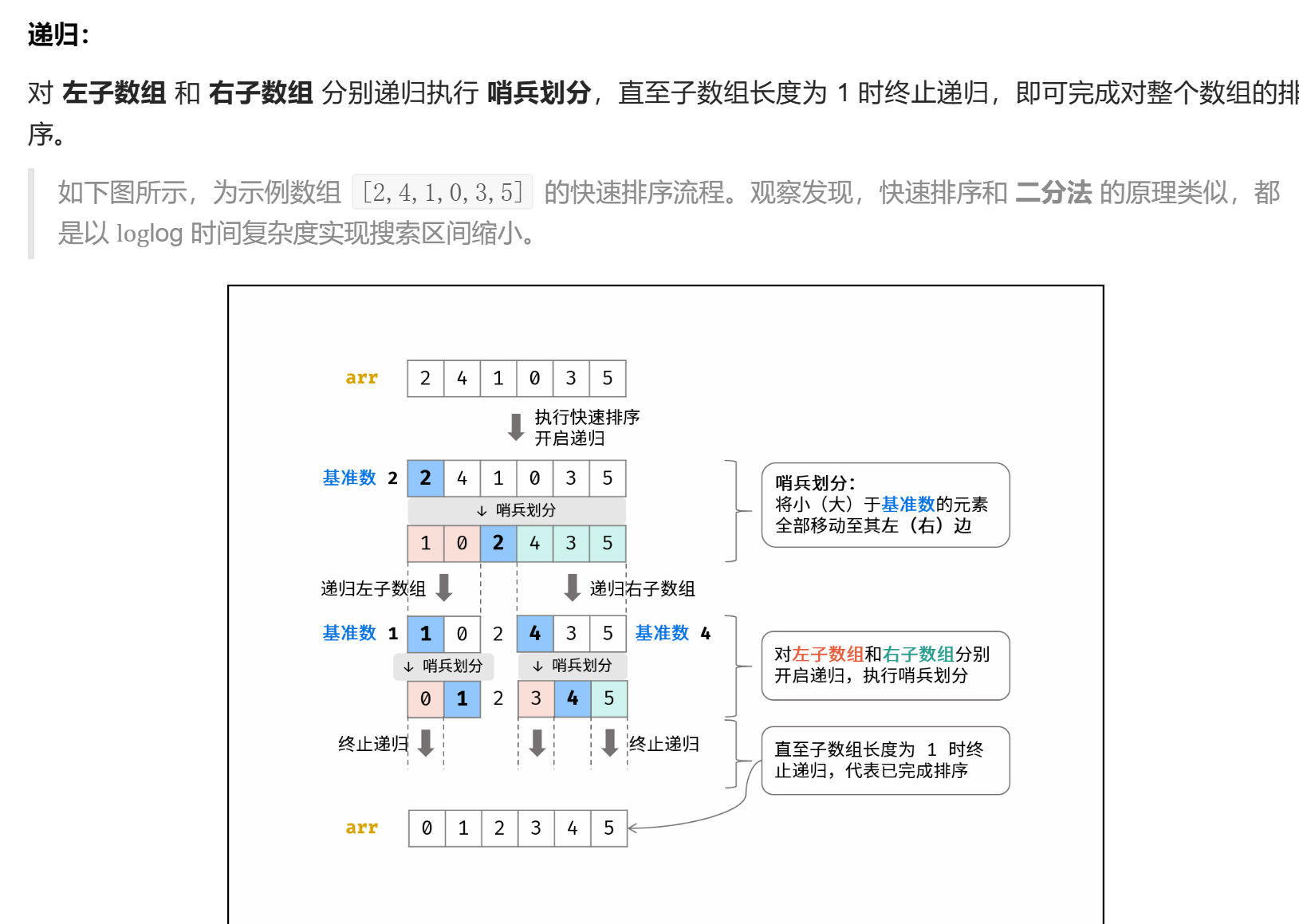
void quickSort(vector<int>& nums, int l, int r) {
    // 子数组长度为 1 时终止递归
    if (l >= r) return;
    // 哨兵划分操作
    int i = partition(nums, l, r);
    // 递归左（右）子数组执行哨兵划分
    quickSort(nums, l, i - 1);
    quickSort(nums, i + 1, r);
}
// 调用
vector<int> nums = { 4, 1, 3, 2, 5, 1 };
quickSort(nums, 0, nums.size() - 1);
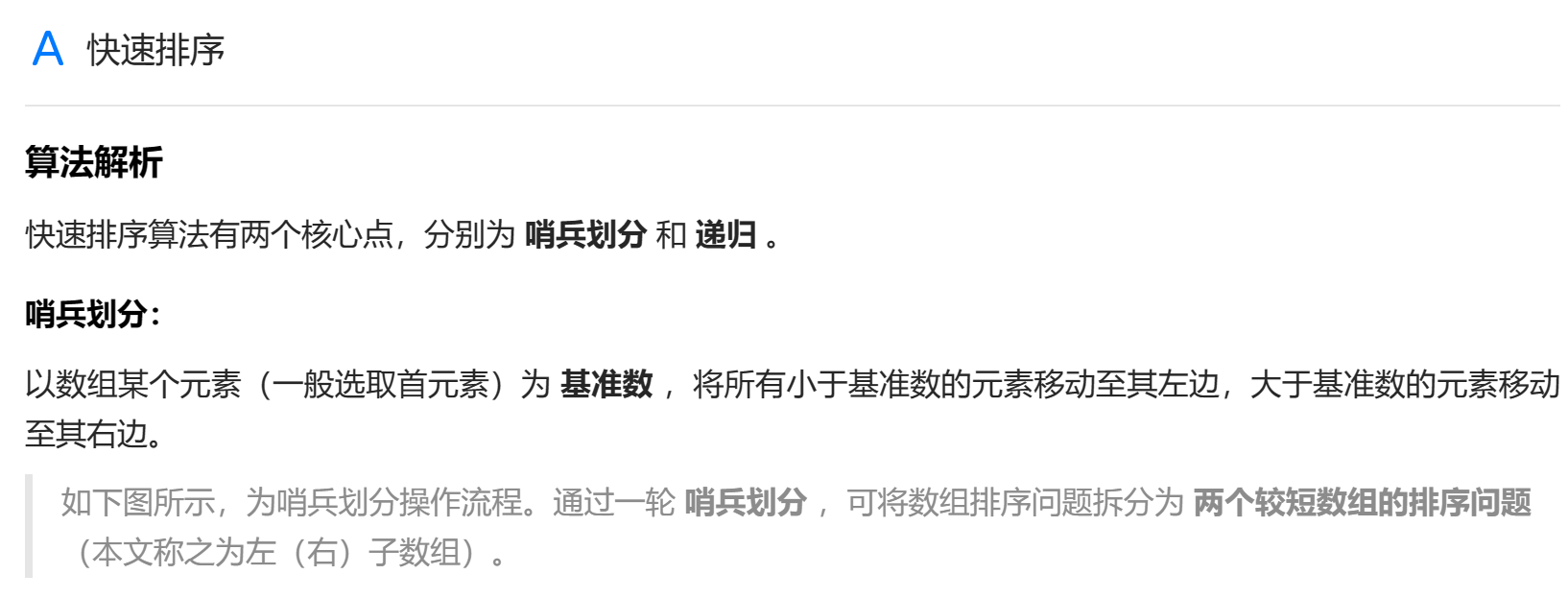
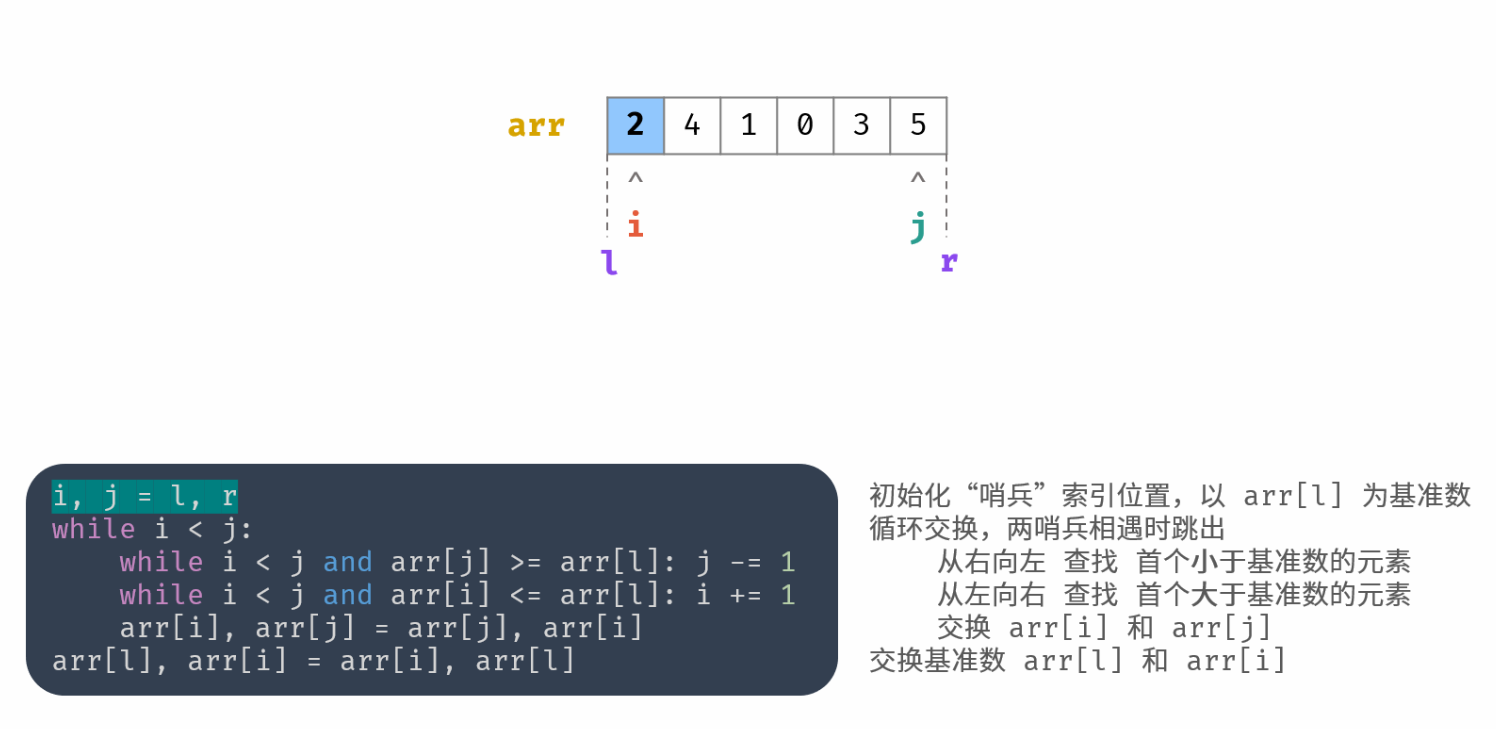
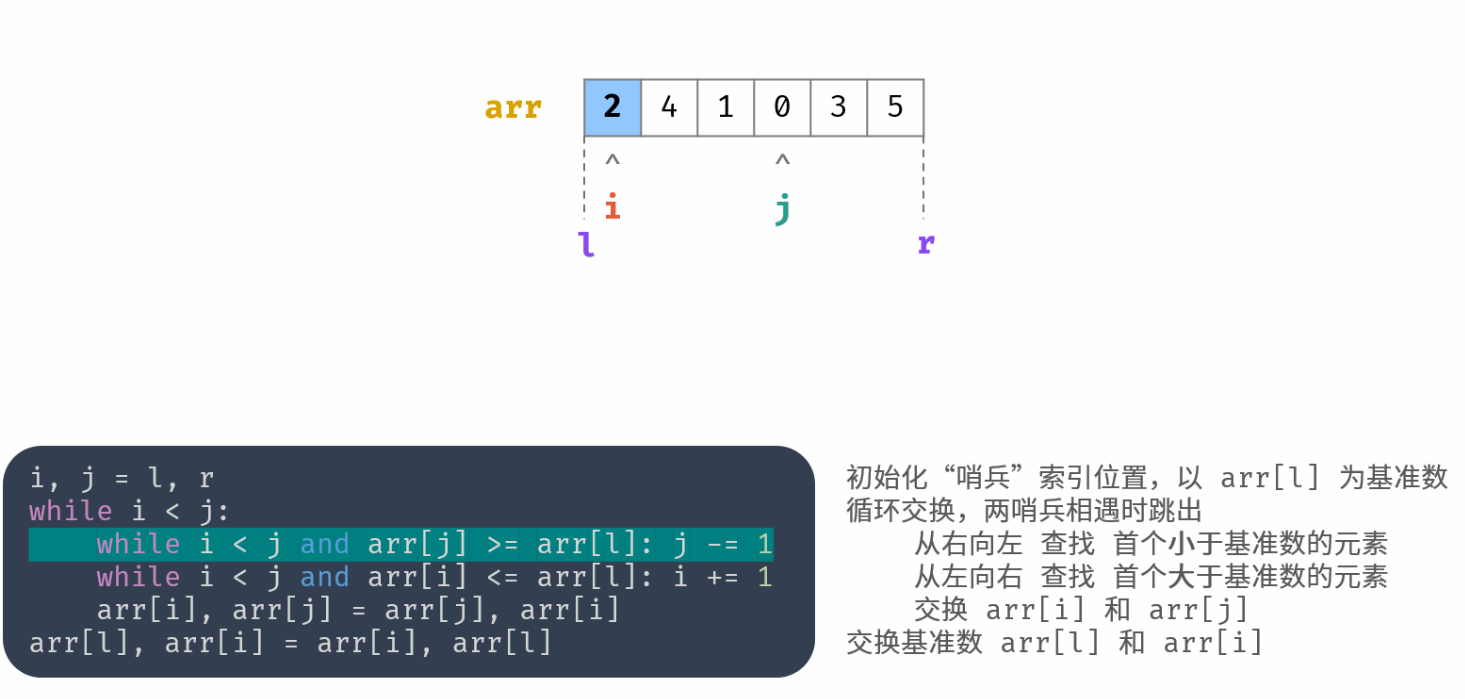
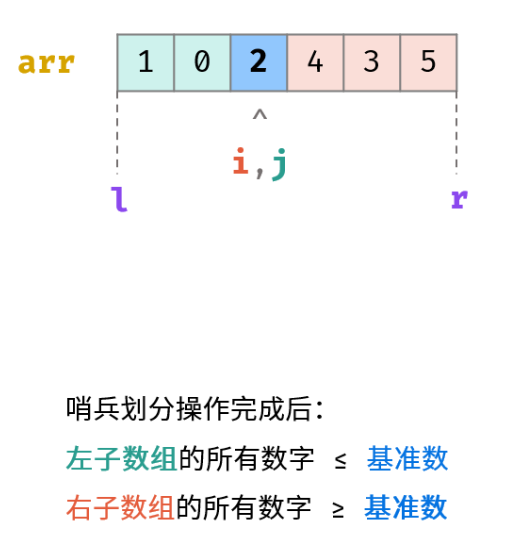
l 和 r 分别是待排序数组的闭区间的左下标和右下标
在第一个对 i 的 while 循环中，必定会使 i 增 1。
外层 while 循环终止的时刻必定有 i=j，
i 和 j 到达同一个位置
i 和 j 到达相邻位置呢？这样会再次进入 while 循环，j 再次自减
两个内层 while 循环可以互换吗？ 可以
在循环最后一个有一个 swap，
里面两个 while 小循环要加上 i<j 的条件，否则，如果遇到剩余的未遍历元素的值等于基准值时，在执行完两个 while 小循环后，会出现 i>j 的情况。
最后 i 和 j 停止的位置的数组值比基准值小，
两个内层 while 循环用的是大于等于和小于等于号，因为关键是找到首个小于或首个大于。
# 归并排序
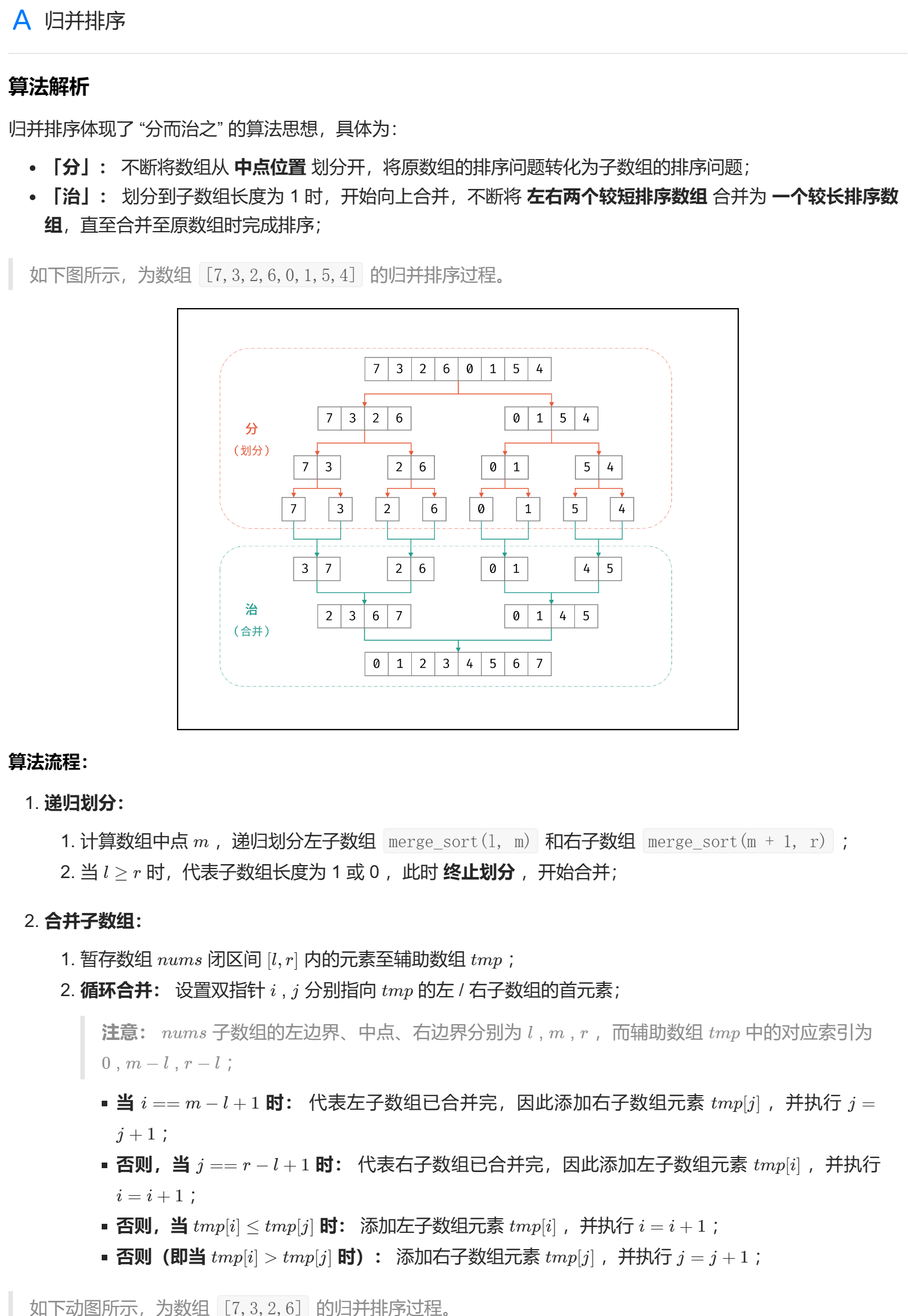
1692194249611
//l，r 为待排序数组（闭区间）的左右下标
void mergeSort(vector<int>& nums, int l, int r) {
    // 终止条件
    if (l >= r) return;
    // 递归划分
    int m = (l + r) / 2;
    mergeSort(nums, l, m);
    mergeSort(nums, m + 1, r);
    // 合并阶段
    int tmp[r - l + 1];             // 暂存需合并区间元素
    for (int k = l; k <= r; k++)
        tmp[k - l] = nums[k];
    int i = 0, j = m - l + 1;       // 两指针分别指向左 / 右子数组的首个元素
    for (int k = l; k <= r; k++) {  // 遍历合并左 / 右子数组
        if (i == m - l + 1)
            nums[k] = tmp[j++];
        else if (j == r - l + 1 || tmp[i] <= tmp[j])
            nums[k] = tmp[i++];
        else {
            nums[k] = tmp[j++];
        }
    }
}
// 调用
vector<int> nums = { 4, 1, 3, 2, 5, 1 };
mergeSort(nums, 0, nums.size() - 1);
1692195248013
vector 没有切片方法，所以要传入待排序的左右下标
void merge_sort(vector<int> &nums, int l, int r) {
    if (l >= r)
        return;
    int m = (l + r) / 2;
    merge_sort(nums, l, m);
    merge_sort(nums, m + 1, r);
    //int temp[r - l + 1];
    vector<int> temp;
    for (int i = 0; i < r - l + 1; i++) {
        //temp[i] = nums[l + i];
        temp.push_back(nums[l + i]);
    }
    int i = 0, j = m - l + 1;
    for (int k = l; k <= r; k++) {
        if (j >= r - l + 1 || temp[i] <= temp[j]) {
            nums[k] = temp[i++];
        }
        else {
            nums[k] = temp[j++];
        }
    }
}
# 剑指 Offer 61. 扑克牌中的顺子
1692201901262
class Solution {
public:
    bool isStraight(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        int zero_count = 0;
        int index = 0;
        // 统计 0 的数量，并使 index 指向第一个非 0 元素
        for (; index < nums.size(); index++) {
            if (nums[index] == 0) {
                zero_count++;
            }
            else {
                break;
            }
        }
        int gap_count = 0; // 统计差的
        for (; index < nums.size() - 1; index++) {
            // 有元素相同的，必定为 false
            if (nums[index + 1] == nums[index]) {
                return false;
            }
            gap_count += nums[index + 1] - nums[index] - 1;
        }
        if (zero_count >= gap_count) {
            return true;
        }
        else {
            return false;
        }
    }
};
1692201931376
class Solution {
public:
    bool isStraight(vector<int>& nums) {
        unordered_set<int> repeat;
        int ma = 0, mi = 14;  // 这里最大值和最小值的初始值设置为范围之外的值
        for(int num : nums) {
            if(num == 0) continue; // 跳过大小王
            ma = max(ma, num); // 最大牌
            mi = min(mi, num); // 最小牌
            if(repeat.find(num) != repeat.end()) return false; // 若有重复，提前返回 false
            repeat.insert(num); // 添加此牌至 Set
        }
        return ma - mi < 5; // 最大牌 - 最小牌 < 5 则可构成顺子
    }
};
class Solution {
public:
    bool isStraight(vector<int>& nums) {
        
        set<int> st;
        int ma = 0, mi = 0;
        bool is_first = true;
        for (int num : nums) {
            if (num != 0) {
                if (st.find(num) == st.end()) {
                    st.insert(num);
                    if (is_first) {
                        ma = mi = num;
                        is_first = false;
                    }
                    else {
                        ma = max(ma, num);
                        mi = min(mi, num);
                    }                    
                }
                else {
                    return false;
                }
            }
        }
        return ma - mi < 5;
    }
};
1692202017170
class Solution {
public:
    bool isStraight(vector<int>& nums) {
        int joker = 0;
        sort(nums.begin(), nums.end()); // 数组排序
        for(int i = 0; i < 4; i++) {
            if(nums[i] == 0) joker++; // 统计大小王数量
            else if(nums[i] == nums[i + 1]) return false; // 若有重复，提前返回 false
        }
        return nums[4] - nums[joker] < 5; // 最大牌 - 最小牌 < 5 则可构成顺子
    }
};
# 剑指 Offer 45. 把数组排成最小的数
1692203229613
1692203328379
class Solution {
public:
    string minNumber(vector<int>& nums) {
        vector<string> strs;
        string res;
        for(int i = 0; i < nums.size(); i++)
            strs.push_back(to_string(nums[i]));
        sort(strs.begin(), strs.end(), [](string& x, string& y){ return x + y < y + x; });
        for(int i = 0; i < strs.size(); i++)
            res.append(strs[i]);
        return res;
    }
};
class Solution {
public:
    string minNumber(vector<int> &nums) {
        vector<string> strs;
        for (int num: nums) {
            strs.push_back(to_string(num));
        }
        sort(strs.begin(), strs.end(), cmp);
        
        string res = "";
        
        for(string item:strs){
            res += item;
        }
        
        return res;
    }
private:
    static bool cmp(string x, string y) {
        return x + y < y + x;
    }
};
# 剑指 Offer 41. 数据流中的中位数
1692260266579
class MedianFinder {
public:
    /** initialize your data structure here. */
    MedianFinder() {
    }
    void addNum(int num) {
        if (ve.size() == 0) {
            ve.push_back(num);
        } else {
            vector<int>::iterator it = ve.begin();
            bool is_insert = false;
            for (; it != ve.end(); it++) {
                // 遇到第一个大于 num 的元素，则在此插入，
                if (*it > num) {
                    ve.insert(it, num);
                    is_insert = true;
                    break;
                }
            }
            if (!is_insert) {
                ve.push_back(num);
            }
        }
    }
    double findMedian() {
        double res = 0;
        if (ve.size() == 0) {
            return res;
        } else if (ve.size() % 2 == 0) {
            int i = ve.size() / 2 - 1;
            int j = i + 1;
            res = ve[i] + ve[j];
            res = res / 2;
            return res;
        }else {
            int i = ve.size() / 2;
            res = ve[i];
            return res;
        }
    }
private:
    vector<int> ve;
};
/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder* obj = new MedianFinder();
 * obj->addNum(num);
 * double param_2 = obj->findMedian();
 */
1692262038801
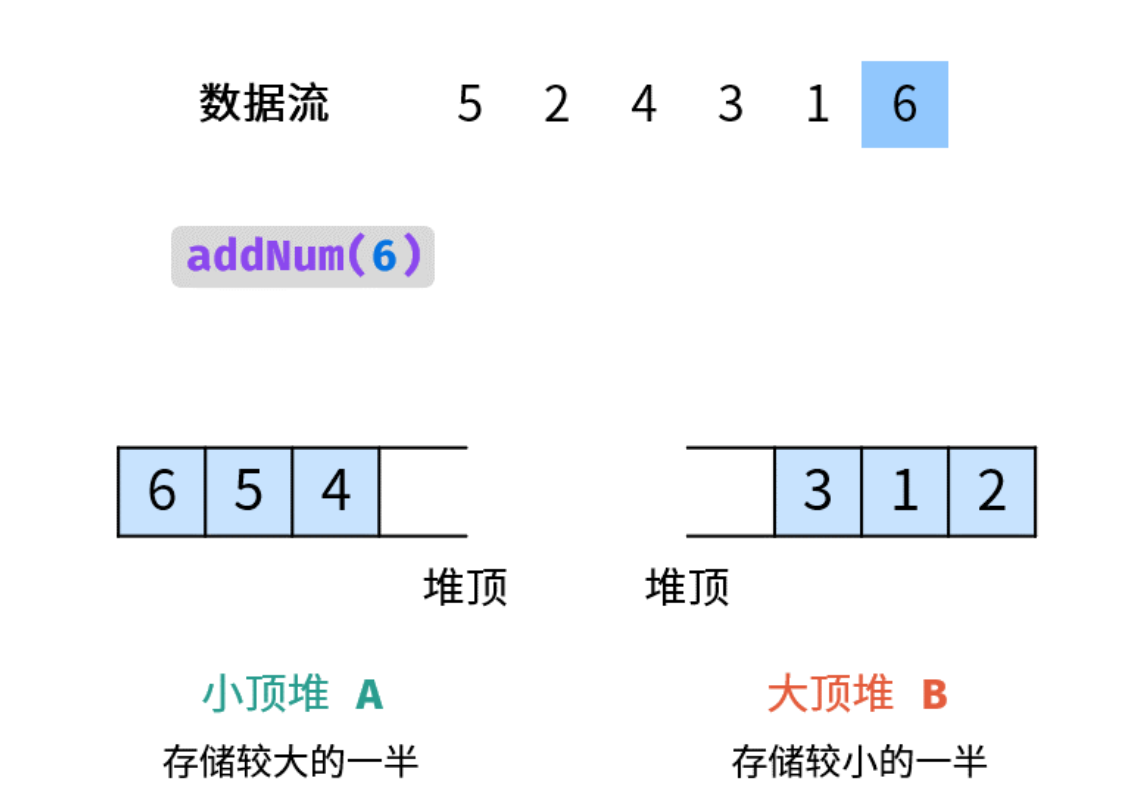
1692262070556
1692262079245
class MedianFinder {
public:
    priority_queue<int, vector<int>, greater<int>> A; // 小顶堆，保存较大的一半
    priority_queue<int, vector<int>, less<int>> B; // 大顶堆，保存较小的一半
    MedianFinder() { }
    void addNum(int num) {
        if(A.size() != B.size()) {
            A.push(num);
            B.push(A.top());
            A.pop();
        } else {
            B.push(num);
            A.push(B.top());
            B.pop();
        }
    }
    double findMedian() {
        return A.size() != B.size() ? A.top() : (A.top() + B.top()) / 2.0;
    }
};
第一次 addNum 的时候，A.size () 和 B.size () 相等，所以最终 A 入队，然后不等，B 入队，导致又相等，如此循环，要么 A.size () 比 B.size () 多 1，要么相等。
  • 怎么保证小顶堆和大顶堆分别是对半排序、且组成的正好是全部元素，而不会重复或其他错误呢？
  • 归纳法，假设小顶堆 A 和大顶堆 B 的 size 相同且已经排好序，并不是将新元素 num 直接压入 A 中，而是将 num 先压入 B 中排序好后将 B 堆顶元素（最大值，必定属于 A）压入 A 中并出队。
# 剑指 Offer 40. 最小的 k 个数
1692262234303
class Solution {
public:
    vector<int> getLeastNumbers(vector<int>& arr, int k) {
        if (k >= arr.size()) return arr;
        return quickSort(arr, k, 0, arr.size() - 1);
    }
private:
    vector<int> quickSort(vector<int>& arr, int k, int l, int r) {
        int i = l, j = r;
        while (i < j) {
            while (i < j && arr[j] >= arr[l]) j--;
            while (i < j && arr[i] <= arr[l]) i++;
            swap(arr[i], arr[j]);
        }
        swap(arr[i], arr[l]);
        if (i > k) return quickSort(arr, k, l, i - 1);
        if (i < k) return quickSort(arr, k, i + 1, r);
        vector<int> res;
        res.assign(arr.begin(), arr.begin() + k);
        return res;
    }
};
注意上面 vector 的 assign 函数。