11-妙用数据结构 - leetCode - algorithm - computer-science | Mi Manchi = yuan = Whatever is worth doing at all is worth doing well

# 内容

C++ STL
数组
栈和队列
单调栈
优先队列
双端队列
哈希表
多重集合和映射
前缀和与积分图

# C++ STL

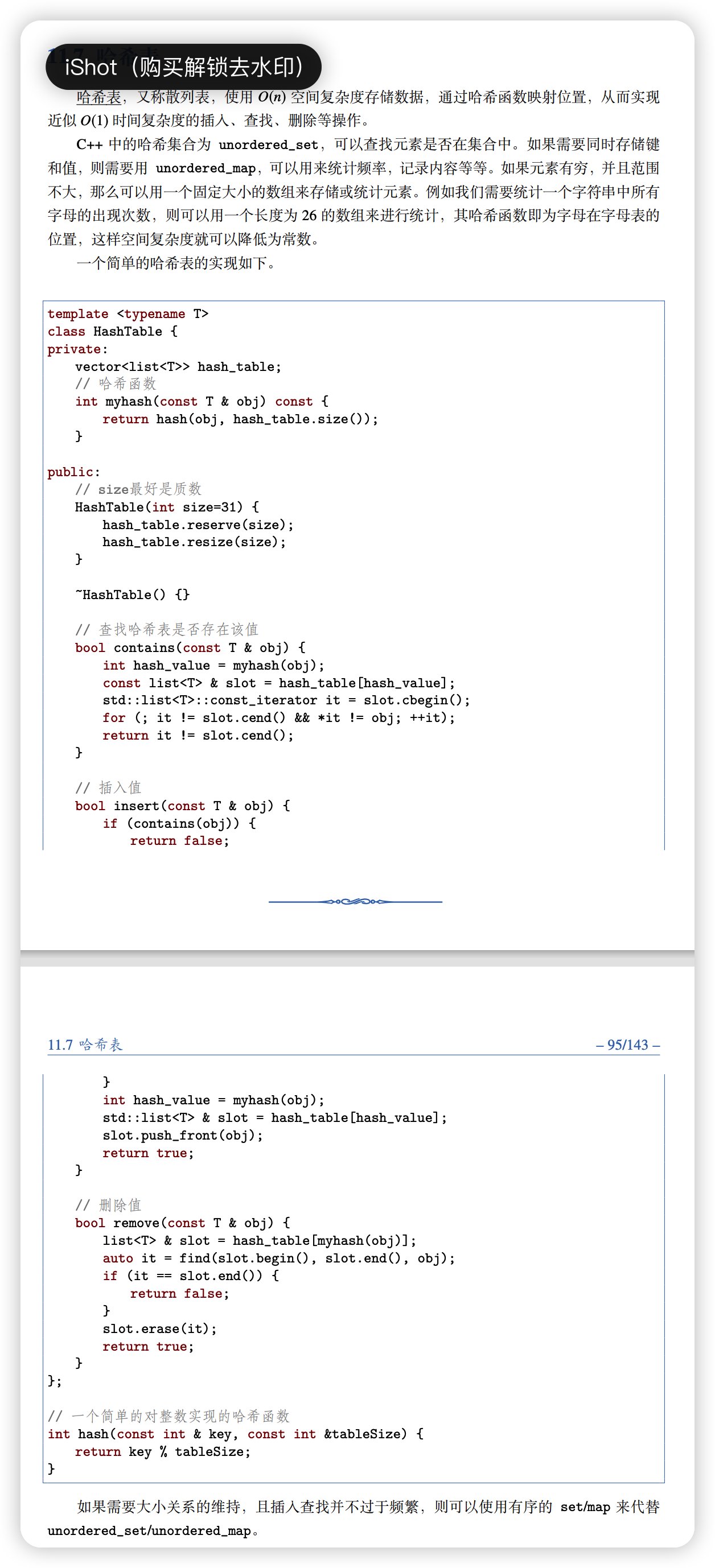
在刷题时，我们几乎一定会用到各种数据结构来辅助我们解决问题，因此我们必须熟悉各种数据结构的特点。C++ STL 提供的数据结构包括（实际底层细节可能因编译器而异）：

Sequence Containers：维持顺序的容器。
1. vector：动态数组，是我们最常使用的数据结构之一，用于 O (1) 的随机读取。因为大

# 数组

# 448. Find All Numbers Disappeared in an Array (Easy)

https://leetcode.com/problems/find-all-numbers-disappeared-in-an-array/

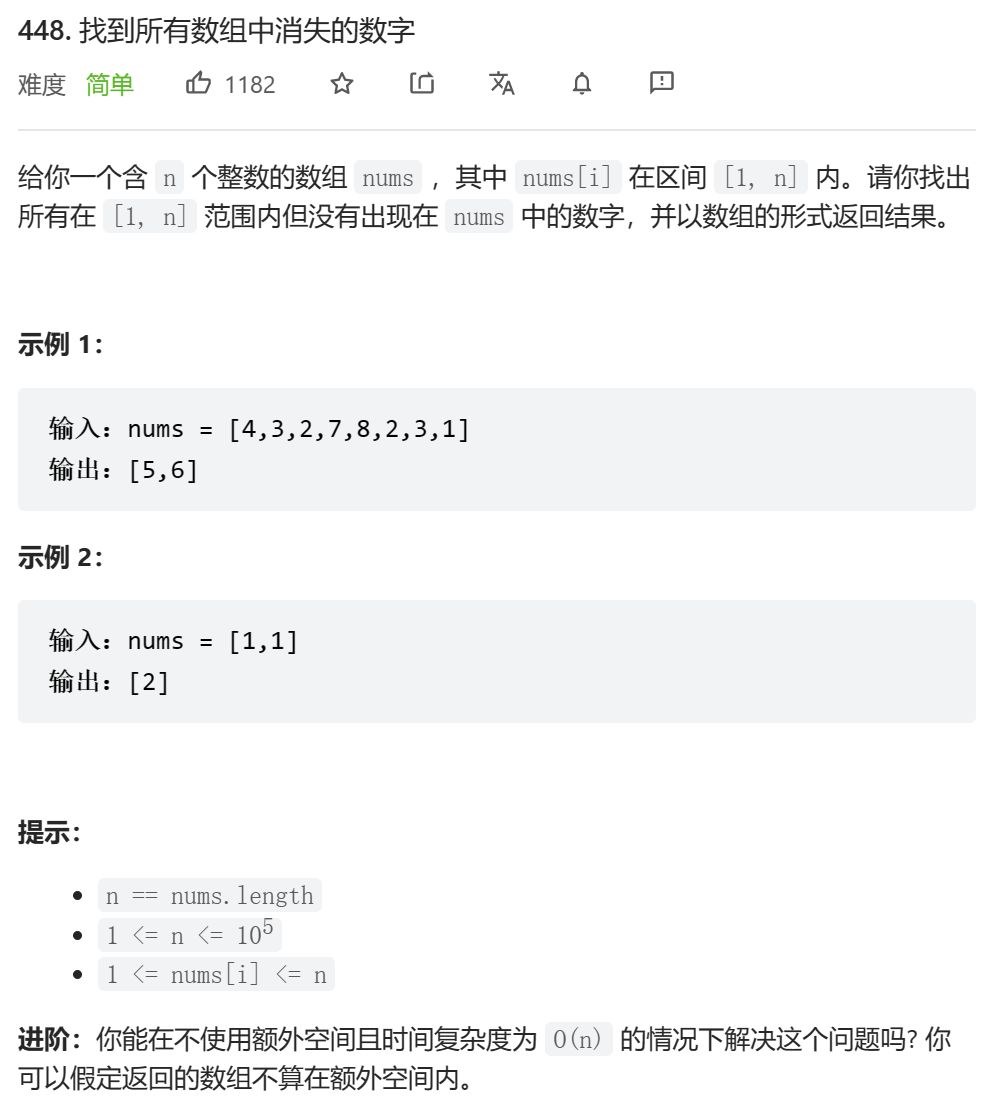
1677931028706

关注进阶处，不使用额外空间。

# 题解

利用数组这种数据结构建立 n 个桶，把所有重复出现的位置进行标记，然后再遍历一遍数组，即可找到没有出现过的数字。进一步地，我们可以直接对原数组进行标记：把重复出现的数字在原数组出现的位置设为负数，最后仍然为正数的位置即为没有出现过的数。

因为要求不使用额外空间，那么就只能在原来的数组上做标记；又因为原数组保存的值都是有用的，或者说其有用性不明。所以选择用负数的形式作为标记，之后再用到这个值的时候，取 abs 绝对值即可。

更改数字的范围为 0~n-1，使用这些作为数组下标，当数组在这些位置上的值小于 0 的时候，说明满足。大于 0 的时候，说明不满足，把下标加 1 后放入结果 vector 中。（不会出现为 0 的情况）

产生问题的原因是数组中会出现重复的数字，因此在遍历原数组的时候会出现重复标记的问题，所以在标记的时候要先判断数组上的数是否大于 0，如果小于 0，说明已经被标记过了，不能重复标记。（两次会负负得正）

	class Solution {
	public:
	vector<int> findDisappearedNumbers(vector<int>& nums) {
	vector<int> ans;

	for (int& num : nums) {
	int pos = abs(num) - 1;
	if (nums[pos] > 0) {
	nums[pos] = -nums[pos];
	}
	}

	for (int i = 0; i < nums.size(); i++) {
	if (nums[i] > 0) {
	ans.push_back(i + 1);
	}
	}

	return ans;
	}
	};

# 48. Rotate Image (Medium)

https://leetcode.com/problems/rotate-image/

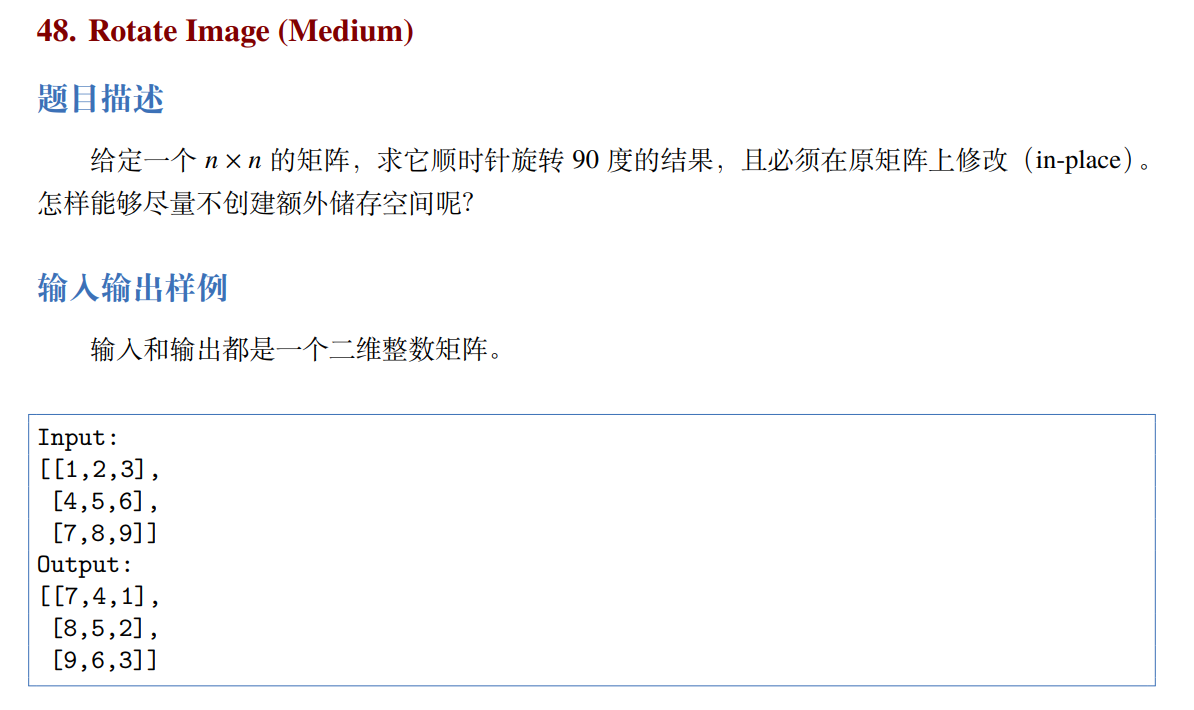
1677932996081

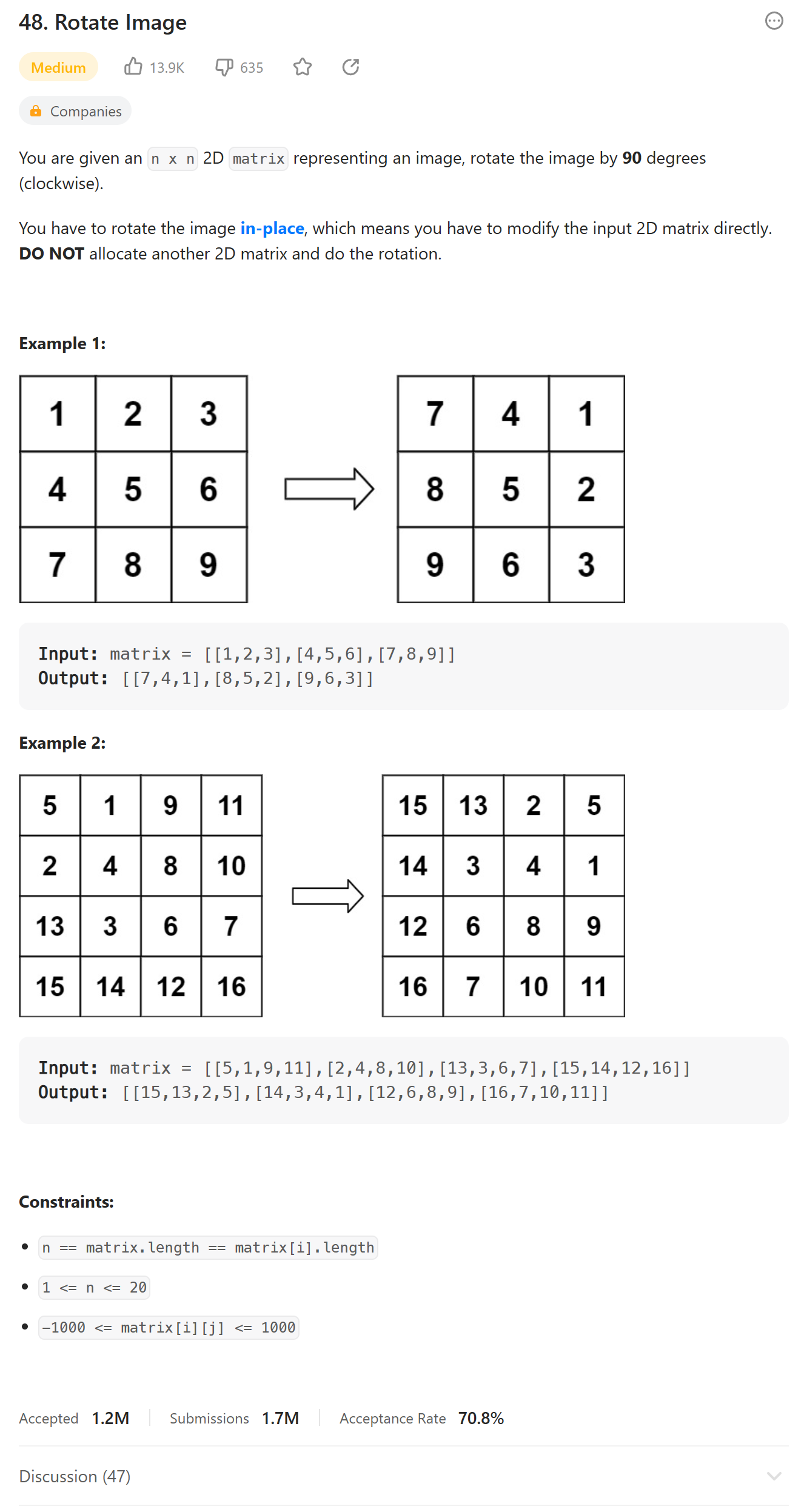
1677933030195

0,0 0,2 2,2 2,0

0,1 1,2 2,1 1,0

0,0 0,3 3,3 3,0
0,1 1,3

1,1 1,2 2,2 2,1

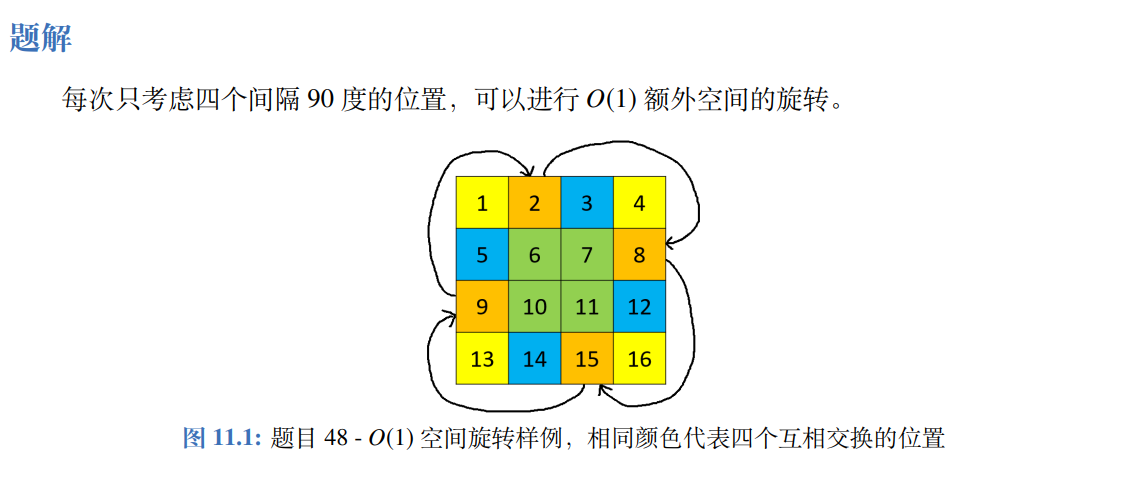
1677938683731

# 想法一

整体是一圈一圈的旋转，有两个循环，外层循环控制圈的数量，内层循环控制一行上移动的数字的个数或者是到边缘的距离。

圈数同时也是每次转动一圈时最上角的横纵坐标。

	class Solution {
	public:
	void rotate(vector<vector<int>>& matrix) {
	int n = matrix.size();

	for (int i = 0; i < n / 2; i++) {
	// 一共有 n/2 圈要转动

	for (int j = 0; j < n - 2 * i - 1; j++) {
	// i,i+j i+j,n-i-1 n-i-1,n-i-1-j n-i-1-j,i
	// 注意：一定要写出上面的坐标变换再写下面的代码
	// 否则，一上来就写下面的代码，边写边想很容易乱掉

	int temp = matrix[n - i - 1 - j][i];

	matrix[n - i - 1 - j][i] = matrix[n - i - 1][n - i - j - 1];
	matrix[n - i - 1][n - i - j - 1] = matrix[i + j][n - i - 1];
	matrix[i + j][n - i - 1] = matrix[i][i + j];

	matrix[i][i + j] = temp;
	}
	}
	}
	};

# 想法二

他这里是用外层循环控制圈数和每一圈中到边缘的距离，内层循环控制转动一圈过程中，一条移动的数的位置（顺便控制了个数）

	class Solution {
	public:
	void rotate(vector<vector<int>>& matrix) {
	int temp = 0, n = matrix.size() - 1;

	//i 为循环的圈数，分别思考 n 为奇数和偶数时都用的 n/2 都对的原理
	//j 为循环时上行的横坐标，i 为纵坐标左上角
	for (int i = 0; i <= n / 2; i++) {
	for(int j = i; j < n - i; j++) {

	//i 代表左上角的位置的横纵坐标
	//i 同时代表横到最上或最下横的距离或者纵到最左或最右纵的距离

	temp = matrix[i][j];

	matrix[i][j] = matrix[n- j][i];
	matrix[n- j][i] = matrix[n-i][n-j];
	matrix[n-i][n-j] = matrix[j][n-i];
	matrix[j][n-i] = temp;

	}
	}
	}
	};


	// 稍微改了一下

	/**
	上下的区别主要是 n 的意义，上面的直接表示最右边的下标，下面的表示长度。
	*/

	class Solution {
	public:
	void rotate(vector<vector<int>>& matrix) {
	int temp = 0, n = matrix.size();

	//i 为循环的圈数，分别思考 n 为奇数和偶数时都用的 n/2 都对的原理
	//j 为循环时上行的横坐标，i 为纵坐标左上角
	for (int i = 0; i < n / 2; i++) {
	for(int j = i; j < n - 1 - i; j++) {

	//i 代表左上角的位置的横纵坐标
	//i 同时代表横到最上或最下横的距离或者纵到最左或最右纵的距离

	temp = matrix[i][j];

	matrix[i][j] = matrix[n- 1- j][i];
	matrix[n- 1- j][i] = matrix[n- 1-i][n- 1-j];
	matrix[n- 1-i][n- 1-j] = matrix[j][n- 1-i];
	matrix[j][n- 1-i] = temp;

	}
	}
	}
	};

# 240. Search a 2D Matrix II (Medium)

https://leetcode.com/problems/search-a-2d-matrix-ii/

1677938803774

1677938825673

1677939190924

为什么要从右上角开始查找呢？可能是因为这是中间位置吧，这也和坐标的判断有关

当从右上角开始的时候，根据当前值和目标值的大小判断，坐标变换要么向左，要么向下。而如果从左上角开始，当当前值比目标值小的时候，可以向右，也可以向下。

类似的，应该也可以从左下角开始搜索。

	// 从右上角开始搜索
	class Solution {
	public:
	bool searchMatrix(vector<vector<int>>& matrix, int target) {


	//i,j 表示当前要比较的值在矩阵中的横纵坐标，进入 while 循环时是还未判断的
	int i = 0, j = matrix[0].size() - 1;


	while(i < matrix.size() && j >= 0) {
	if(matrix[i][j] == target) {
	return true;
	}else if(matrix[i][j] > target) {
	j--;
	}else{
	i++;
	}
	}

	return false;
	}
	};



	// 从左下角开始搜索
	class Solution {
	public:
	bool searchMatrix(vector<vector<int>>& matrix, int target) {

	//i,j 表示当前要比较的值在矩阵中的横纵坐标，进入 while 循环时是还未判断的
	int i = matrix.size() - 1, j = 0;

	while(i >= 0 && j < matrix[0].size()) {
	if(matrix[i][j] == target) {
	return true;
	}else if(matrix[i][j] > target) {
	i--;
	}else{
	j++;
	}
	}

	return false;
	}
	};

# 769. Max Chunks To Make Sorted (Medium)

https://leetcode.com/problems/max-chunks-to-make-sorted/

1677944001600

1677944029200

1677944952804

	class Solution {
	public:
	int maxChunksToSorted(vector<int>& arr) {
	int temp_max = arr[0];
	int count = 0;

	for(int i = 0; i < arr.size(); i++) {
	if(temp_max < arr[i]) {
	temp_max = arr[i];
	}

	if(temp_max == i) {
	count++;

	if(i + 1 < arr.size()) {
	temp_max = arr[i + 1];
	}
	}
	}

	return count;
	}
	};

# 栈和队列

# 232. Implement Queue using Stacks (Easy)

https://leetcode.com/problems/implement-queue-using-stacks/

1679101108359

1679101169008

	class MyQueue {
	stack<int> in, out;
	public:
	MyQueue() {

	}

	void push(int x) {
	in.push(x);
	}

	int pop() {
	while(!in.empty()) {
	int temp = in.top();
	out.push(temp);
	in.pop();
	}

	int res = out.top();
	out.pop();

	while(!out.empty()) {
	int temp = out.top();
	in.push(temp);
	out.pop();
	}
	return res;

	}

	int peek() {
	while(!in.empty()) {
	int temp = in.top();
	out.push(temp);
	in.pop();
	}

	int res = out.top();

	while(!out.empty()) {
	int temp = out.top();
	in.push(temp);
	out.pop();
	}
	return res;
	}

	bool empty() {
	return in.empty();
	}
	};

	/**
	* Your MyQueue object will be instantiated and called as such:
	* MyQueue* obj = new MyQueue();
	* obj->push(x);
	* int param_2 = obj->pop();
	* int param_3 = obj->peek();
	* bool param_4 = obj->empty();
	*/

# 155. Min Stack (Easy)

1679102237521

注意：如果只使用一个变量来表示当前栈的最小值，那么每次出栈之后都要重新遍历栈中的全部元素以获得当前栈的最小值，而这是无法仅仅使用一个栈来实现的。

1679102405304

	class MinStack {
	stack<int> s, min_s;

	public:
	MinStack() {

	}

	void push(int val) {
	s.push(val);

	if (min_s.empty() \|\| min_s.top() >= val) {
	min_s.push(val);
	}
	}

	void pop() {
	if (!s.empty()) {
	if (min_s.top() == s.top()) {
	min_s.pop();
	}
	s.pop();
	}

	}

	int top() {
	return s.top();
	}

	int getMin() {
	return min_s.top();
	}
	};

	/**
	* Your MinStack object will be instantiated and called as such:
	* MinStack* obj = new MinStack();
	* obj->push(val);
	* obj->pop();
	* int param_3 = obj->top();
	* int param_4 = obj->getMin();
	*/

# 20. Valid Parentheses (Easy

https://leetcode.com/problems/valid-parentheses/

1679105136627

1679105154305

	class Solution {

	public:
	bool isValid(string s) {
	stack<char> sk;

	set<char> leftChar{'(', '{', '['};
	set<char> rightChar{')', '}', ']'};

	for (int i = 0; i < s.length(); i++) {
	char temp = s[i];

	if (leftChar.find(temp) != leftChar.end()) {
	sk.push(temp);
	} else {
	if(sk.empty()) {
	return false;
	}

	if(temp == ')' && sk.top() == '(' \|\| sk.top() == '{' && temp == '}' \|\| sk.top() == '[' && temp == ']') {
	sk.pop();
	}else {
	return false;
	}
	}
	}

	if(sk.empty()) {
	return true;
	}else {
	return false;
	}


	}
	};

# 单调栈

单调栈通过维持栈内值的单调递增（递减）性，在整体 O (n) 的时间内处理需要大小比较的
问题。

# 739. Daily Temperatures (Medium)

https://leetcode.com/problems/daily-temperatures/

1679106009744

1679106026191

1679106877051

单调栈并非对所有的数据进行排序后放到栈中，而是针对原序列，

	class Solution {
	public:
	vector<int> dailyTemperatures(vector<int>& temperatures) {
	stack<int> sk;

	int n = temperatures.size();
	vector<int> ve(n);

	for(int i = 0; i < temperatures.size(); i++) {

	while(!sk.empty()) {
	int pre = sk.top();

	if(temperatures[pre] < temperatures[i]) {
	ve[pre] = i - pre;
	sk.pop();
	}else{
	break;
	}
	}


	sk.push(i);
	}

	return ve;

	}
	};

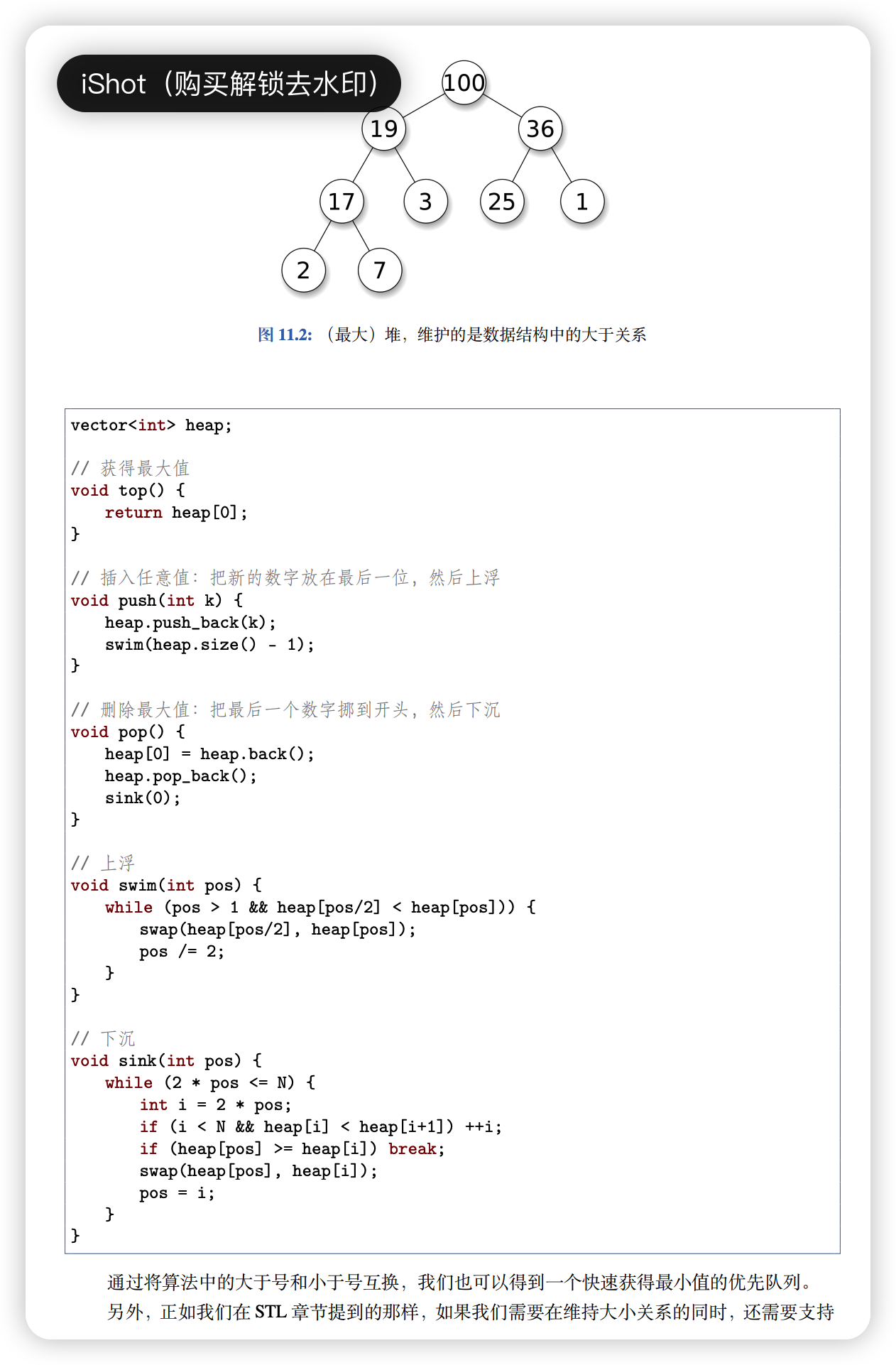
# 11.5 优先队列

1679107809932

1679107837110

1679107854845

# 23. Merge k Sorted Lists (Hard)

https://leetcode.com/problems/merge-k-sorted-lists/

1679109465972

1679109432004

注：因为原先的几条链表本来就是有序的，所有一开始只需要往优先队列加入链表的头结点指针，在之后再逐个加入。不过，一开始就全部加入也是可以的，但可能会因为数量多，在维持堆的结构上花费的时间多一点。

	struct ListNode {
	int val;
	ListNode *next;
	ListNode() : val(0), next(nullptr) {}
	ListNode(int x) : val(x), next(nullptr) {}
	ListNode(int x, ListNode *next) : val(x), next(next) {}
	};



	class Solution {
	public:

	struct cmp{
	bool operator()(ListNode* l1, ListNode* l2) {
	return l1->val > l2->val;
	}
	};

	ListNode* mergeKLists(vector<ListNode*>& lists) {
	priority_queue<ListNode, vector<ListNode> ,cmp> q;

	for(int i = 0; i < lists.size(); i++) {
	ListNode* ptr = lists[i];

	while(ptr != nullptr) {
	q.push(ptr);
	ptr = ptr->next;
	}

	}

	ListNode* p1 = new ListNode(0, nullptr);
	ListNode* p2 = p1;

	while (!q.empty()) {
	p2->next = q.top();
	p2 = p2->next;

	p2->next = nullptr;

	q.pop();
	}
	return p1->next;

	}
	};

# 218. The Skyline Problem (Hard)

https://leetcode.com/problems/the-skyline-problem/

未做

# 哈希表

1679111642005

# 1. Two Sum (Easy)

https://leetcode.com/problems/two-sum/

1679112372946

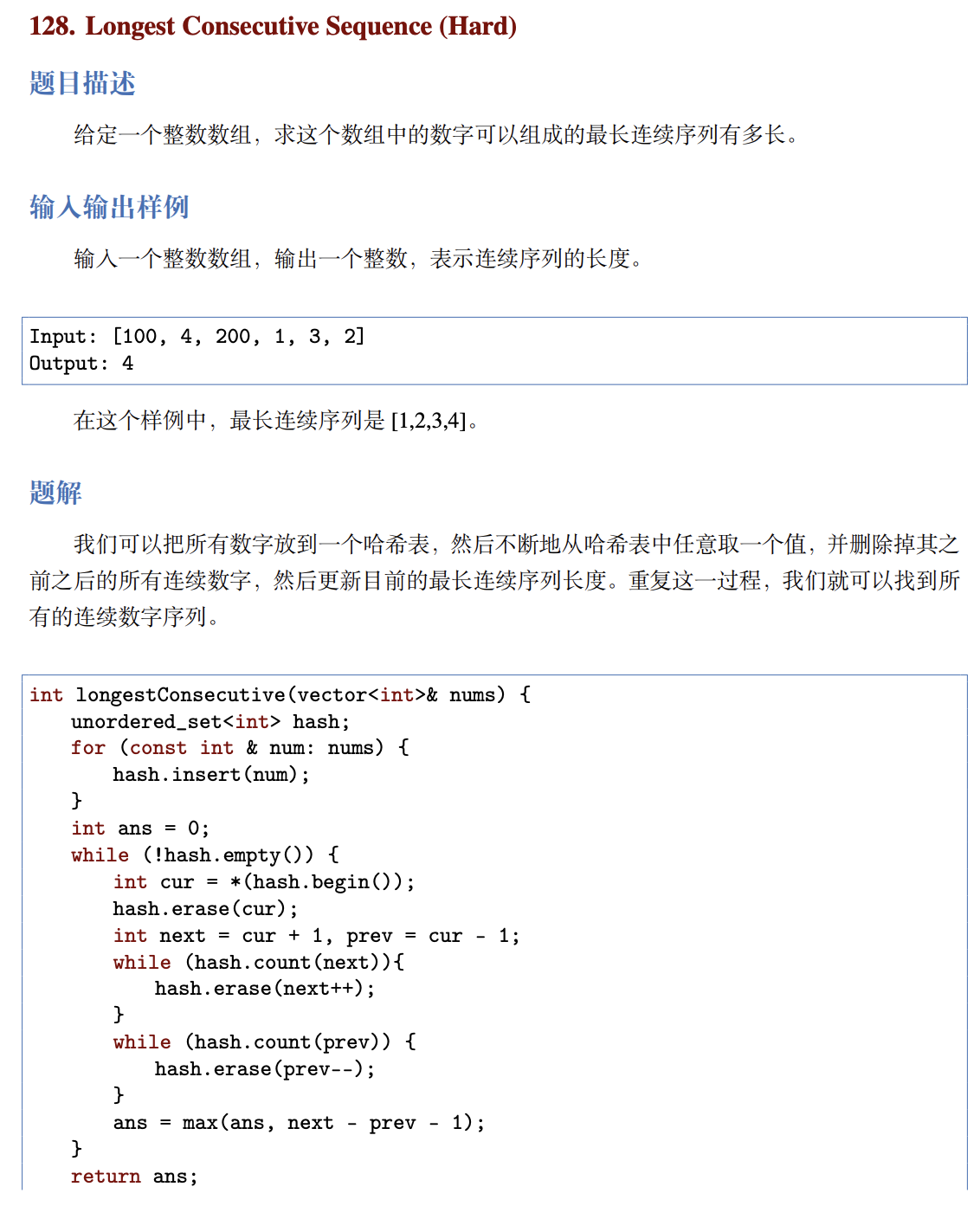
# 128. Longest Consecutive Sequence (Hard)

https://leetcode.com/problems/longest-consecutive-sequence/

1679113025752

# 多重集合和映射

# 332. Reconstruct Itinerary (Medium)

https://leetcode.com/problems/reconstruct-itinerary/

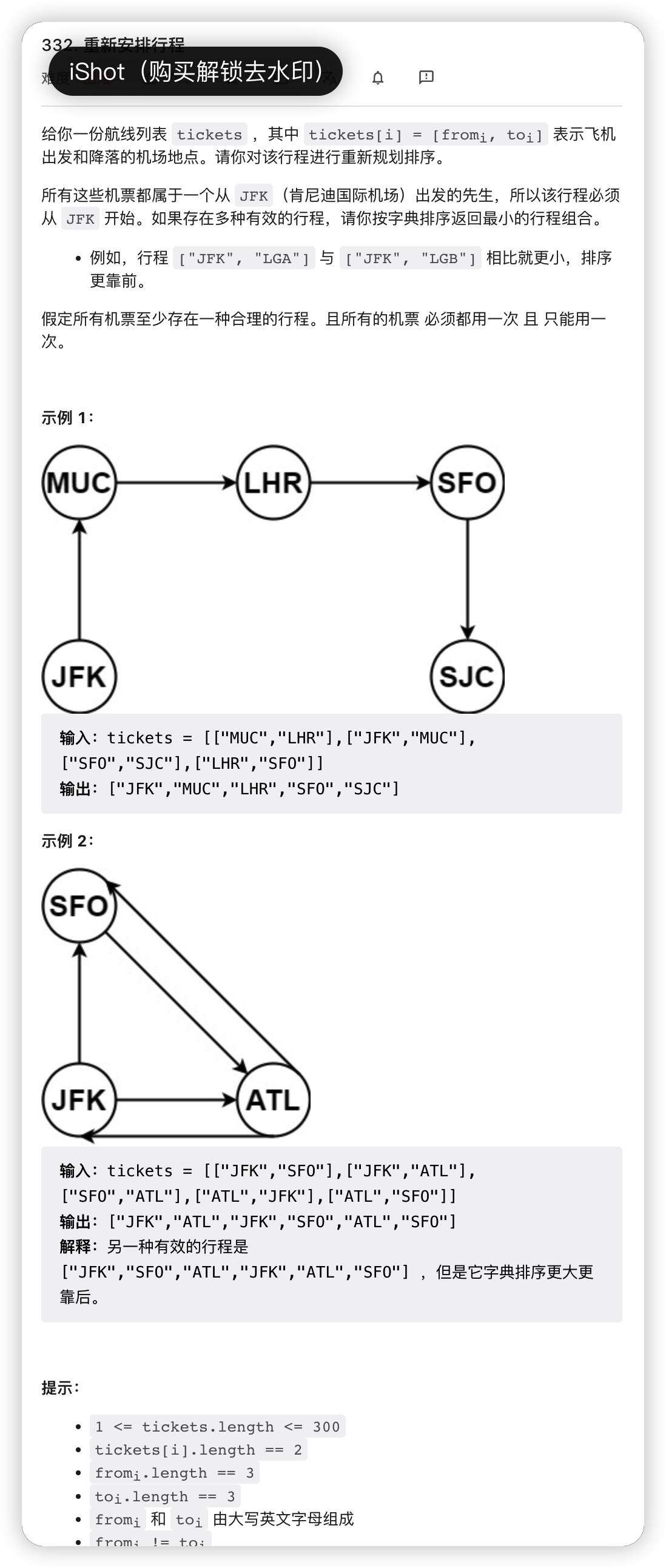
1679326033046

这里用的类似 bfs 类似的思想吗？当只存在键而没有存在值的时候就加入结果 vector 中。

又不是 bfs，因为这里用的是栈而不是队列

multiset 是自动有序的，unordered_map 的键也是有序的

当只存在键而没有存在值的时候就加入结果 vector 中。

导致先进入死胡同是因为字典序靠前的，

这里用的栈，进行的是 dfs

主要是保证出栈的顺序，单条路径进去的得是先出栈，那么就是先进入 ans，之后 ans 反向，最后是单条路径的后面进入。

# 前缀和与积分图

一维的前缀和，二维的积分图，都是把每个位置之前的一维线段或二维矩形预先存储，方便
加速计算。如果需要对前缀和或积分图的值做寻址，则要存在哈希表里；如果要对每个位置记录
前缀和或积分图的值，则可以储存到一维或二维数组里，也常常伴随着动态规划。

# 303. Range Sum Query - Immutable (Easy)

https://leetcode.com/problems/range-sum-query-immutable/

1679113303932

# 560. Subarray Sum Equals K (Medium)

1679318492984

	class Solution {
	public:
	int subarraySum(vector<int>& nums, int k) {
	int pSum = 0, count = 0;
	map<int, int> mp;

	mp[0] = 1;

	for(const int num: nums) {
	pSum += num;
	count += mp[pSum - k];
	mp[pSum]++;
	}

	return count;
	}
	};

注意：nums [i] 和 k 都有可能是负数，因此会存在着这段不同的区间的（前缀）和是相同的情况，所以使用 mp [pSum]++ 而不是 mp [pSum]=1，否则的话，存在 pSum-k 对应多段区间，k 也对应多段区间，造成损失计数。

算法