转载自 https://zhuanlan.zhihu.com/p/476927099
# 分类
分类是机器学习中应用最广泛的问题之一,具有各种工业应用,比如人脸识别、图像分类、内容审核、文本分类等,支持向量机 (SVM)、逻辑回归、决策树、随机森林等模型也是一些最流行的分类模型,那么对于分类问题最常用的指标是:
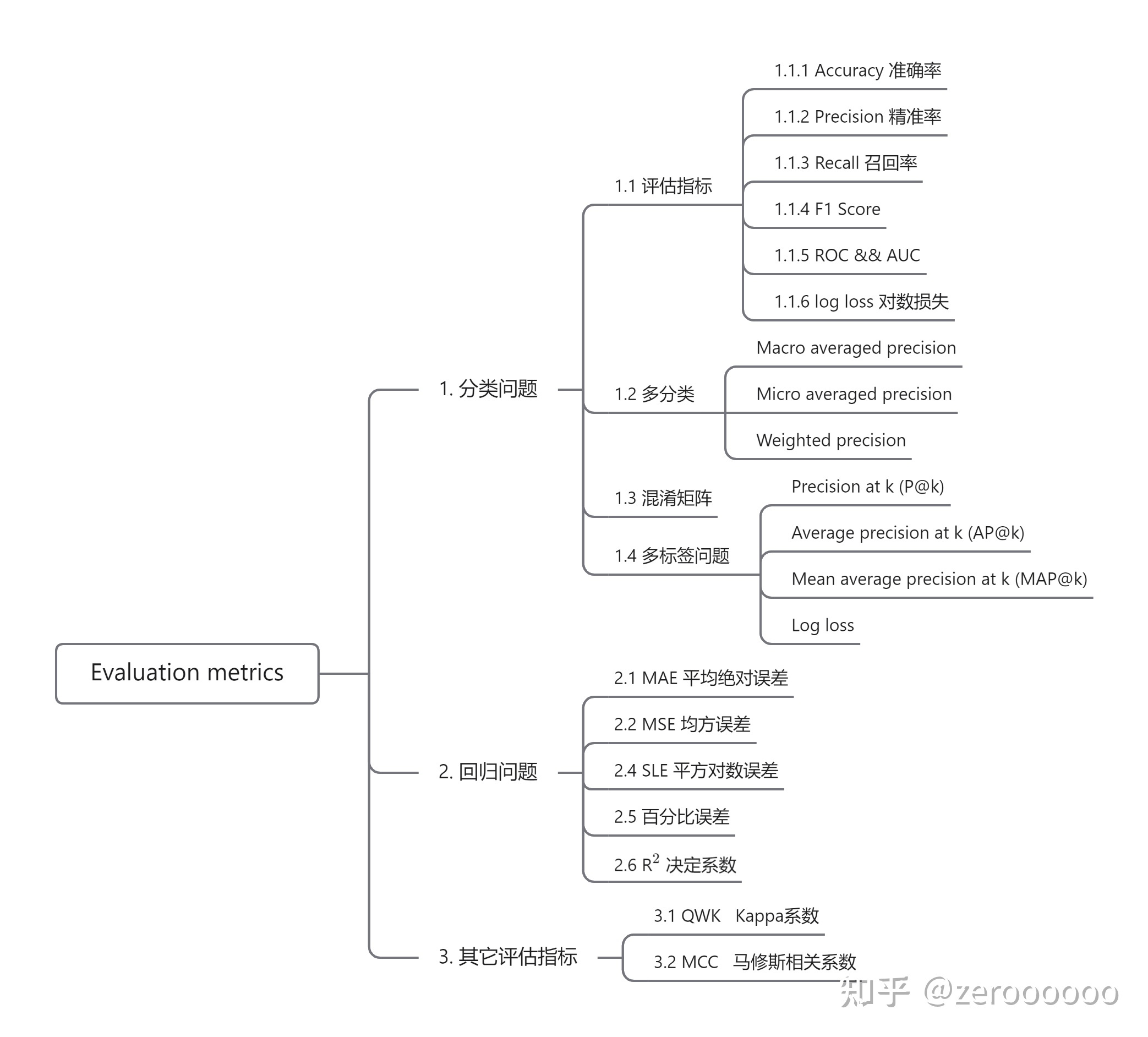
- Accuracy 准确率
- Precision (P) 精准率
- Recall (R) 召回率
- F1 score (F1)
- Area under the ROC (Receiver Operating Characteristic) curve or simply AUC (AUC)
- Log loss 对数损失
- Precision at k (P@k)
- Average precision at k (AP@k)
- Mean average precision at k (MAP@k)
# 回归
回归模型用于预测连续目标值,同样具有广泛的应用,如房价预测、天气预测、股价预测等,线性回归、随机森林、XGboost、循环神经网络等也是一些最流行的回归模型。
用于评估回归模型的指标应该能够处理一组连续值,因此与分类指标略有不同,在回归方面,最常用的评估指标是:
- Mean absolute error (MAE) 平方绝对误差
- Mean squared error (MSE) 均方误差
- Root mean squared error (RMSE) 均方根误差
- Root mean squared logarithmic error (RMSLE)
- Mean percentage error (MPE)
- Mean absolute percentage error (MAPE)
- 决定系数
了解上述指标的工作原理并不是我们唯一需要做的事情,更重要的是要知道何时使用这些指标,这就取决于数据和标签。
另外需要注意的是,评估指标不同于损失函数,损失函数是展示模型性能的函数,用于训练机器学习模型(使用某种优化方法),并且通常在模型的参数上是可微的。 另一方面,评估指标用于监控和衡量模型的性能(在训练和测试期间),并且不必是可微的。 但是,如果对于某些任务,性能指标是可微的,则它既可以用作损失函数(可能添加一些正则化),也可以用作评估指标,例如 MSE。
# 1. 分类问题
为了进一步了解这些指标,我们从一个简单的问题开始。假设我们有一个二分类问题,即一个胸部 x 光图像分类的问题。一些胸部 x 光片显示正常,一些胸部 x 光片显示肺塌陷,也就是气胸。因此,我们的任务是建立一个分类器,在给定的胸部 x 光图像中可以检测出是否有气胸。
假设有同等数量的气胸和非气胸的胸部 X 光图像,比如各 100 张。因此,我们有 100 个正样本和 100 个负样本,总共有 200 张图像。
第一步是将上述数据分成两组相等的 100 张图像,即训练集和验证集。在这两组样本中,我们有 50 个正样本和 50 个负样本。
当我们在二分类问题中有相等数量的正样本和负样本时,我们通常使用的度量指标为 accuracy、precision、recall 和 f1
# 1.1 评估指标
# 1.1.1 Accuracy 准确率
accuracy(准确率):机器学习中最直接的度量指标之一。 它定义了模型有多准确。对于上面描述的问题,如果建立的模型能够准确地对 90 张图片进行分类,那么准确率就是 90% 或 0.90。如果只有 83 张图片被正确分类,则模型的准确率是 83% 或 0.83。
用于计算 accuracy 的 Python 代码也非常简单
def accuracy(y_true, y_pred):
"""
Function to calculate accuracy
:param y_true: 真实值
:param y_pred: 预测值
:return: 准确度
"""
# 初始化计数器
correct_counter = 0
# 遍历真实值和预测值
for yt, yp in zip(y_true, y_pred):
if yt == yp:
# 如果预测正确,计数加一
correct_counter += 1
# 返回准确度
return correct_counter / len(y_true)
我们也可以使用 scikit-learn 工具包来计算准确度
In [X]: from sklearn import metrics
...: l1 = [0,1,1,1,0,0,0,1]
...: l2 = [0,1,0,1,0,1,0,0]
...: metrics.accuracy_score(l1, l2)
Out[X]: 0.625
现在,假设稍微改变一下数据集,有 180 张胸部 x 光图像没有气胸,只有 20 张气胸。即使在这种情况下,也创建具有相同正样本与负样本(气胸与非气胸)目标比率的训练集和验证集。即在每一组中,我们有 90 个非气胸图像和 10 个气胸图像。如果我们直接判断验证集中的所有图像都不是气胸,那么准确度是多少呢?答案是正确分类了 90% 的图像,此时我们的准确率是 90%。
那么问题来了
我们甚至不用创建具体的模型,准确率就达到了 90% ,这样就没有衡量价值了。如果仔细观察就会发现数据集是分布不均的,即一个类中的样本数量比另一个类中的样本数量多很多。在这种情况下,不建议再使用准确率作为评估指标,因为它衡量不出什么。所以,虽然可能得到很高的准确率,但当涉及到真实世界的样本时,模型可能不会表现得那么好。
由于数据的分布不均匀,导致模型在学习的参数上会出现偏颇。
# 1.1.2 Precision 精准率
在这种情况下,最好看看其他指标,比如 precision(精准率,又叫查准率)。
在学习 precision 之前,我们还需要知道一些术语。假设有气胸的胸部 x 光图像为阳性类 (1),无气胸的胸部 x 射线图像为阴性类 (0)。
真阳性(TP):给定一张图像,如果模型预测该图像有气胸,而该图像实际上也有气胸,则该图像被视为真阳性。
真阴性(TN):给定一张图像,如果模型预测该图像非气胸,而实际上也是非气胸图像,则该图像被视为真阴性。
简单来讲,如果模型正确预测了阳性,那就是真阳性,如果模型正确预测了阴性,那就是真阴性
假阳性(FP):给定一张图像,如果模型预测该图像有气胸,而该图像实际上是非气胸,则为假阳性。
假阴性(FN):给定一张图像,如果模型预测该图像非气胸,而该图像实际上是气胸,则为假阴性。
简单来讲,如果模型没有正确预测阳性,那就是假阳性。如果模型没有正确预测阴性,那么就是一个假阴性
让我们看一下这些的实现